はじめて学ぶベクトル空間｜高専・大学

高専・大学数学はじめて学ぶベクトル空間

はじめて学ぶベクトル空間

定価：1,760円（本体1,600円＋税）
体裁：A5判／ 147頁
ISBN：978-4-477-03049-4

執筆
	執筆	碓氷久（群馬工業高等専門学校教授）	高遠節夫（東邦大学理学部訪問教授）	濵口直樹（長野工業高等専門学校教授）
	執筆	松澤寛（神奈川大学理学部准教授）	山下哲（木更津工業高等専門学校教授）
校閲
	校閲	井川治（京都工芸繊維大学大学院教授）	篠原知子（都立産業技術高等専門学校准教授）	下田泰史（仙台高等専門学校准教授）
	校閲	高橋正郎（久留米工業高等専門学校准教授）	三浦崇（鶴岡工業高等専門学校准教授）	森本真理（秋田工業高等専門学校准教授）

「はじめて学ぶベクトル空間」のねらい

高等専門学校の本科で「線形代数」の学習をひと通りすませた学生を対象とした「ベクトル空間」について学ぶ入門書です。
1章は基本事項の簡単な復習となっていて，2章以降で，抽象的と言われるベクトル空間について身近なものから高度なものまで身につけられる構成になっています。
高専の本科や専攻科で，「ベクトル空間」を指導したいとお考えの先生や，大学編入学試験でも出題される「ベクトル空間」について勉強したいという学生の方にお使いいただけます。

目次	1章ベクトル・行列・行列式ベクトルの演算／ベクトルの内積／行列の演算／連立１次方程式と消去法／逆行列／行列式／行列の正則性／ベクトルの線形独立・線形従属／集合
	2章数ベクトル空間数ベクトル空間／線形独立／基底／基底の変換／内積と正規直交基底
	3章線形変換と線形写像線形変換／固有値と固有ベクトル／線形写像
	4章部分空間部分空間の定義／部分空間の基底と次元／線形写像と部分空間／直交補空間
	5章いろいろなベクトル空間一般のベクトル空間／複素数ベクトル空間
	補章ジョルダン標準形２次のジョルダン標準形／３次のジョルダン標準形／n次のジョルダン標準形

専攻科などの授業でも扱える

本科の「線形代数」の授業からの接続に配慮して，１章には基本事項の簡単な復習の章を設けました。進度に応じて２章から進めていただけます。
専攻科などの授業でお使いいただけるように，「ベクトル空間」にポイントを絞って内容を厳選しました。

１章　ベクトル・行列・行列式

本書は，弊社の「新線形代数」の続編として，専攻科の授業や大学編入学試験対策としてお使いいただけます。本科の「線形代数」の授業を前提としていますが，１章に基本事項の簡単な復習を設けました。

ベクトル空間の身近なものから高度なものまで身につけられる

抽象的と言われるベクトル空間を，わかりやすい具体例で解説するとともに，ベクトル空間の身近なものから高度なものまで段階的に身につけられるように丁寧な構成にしました。

２章　数ベクトル空間

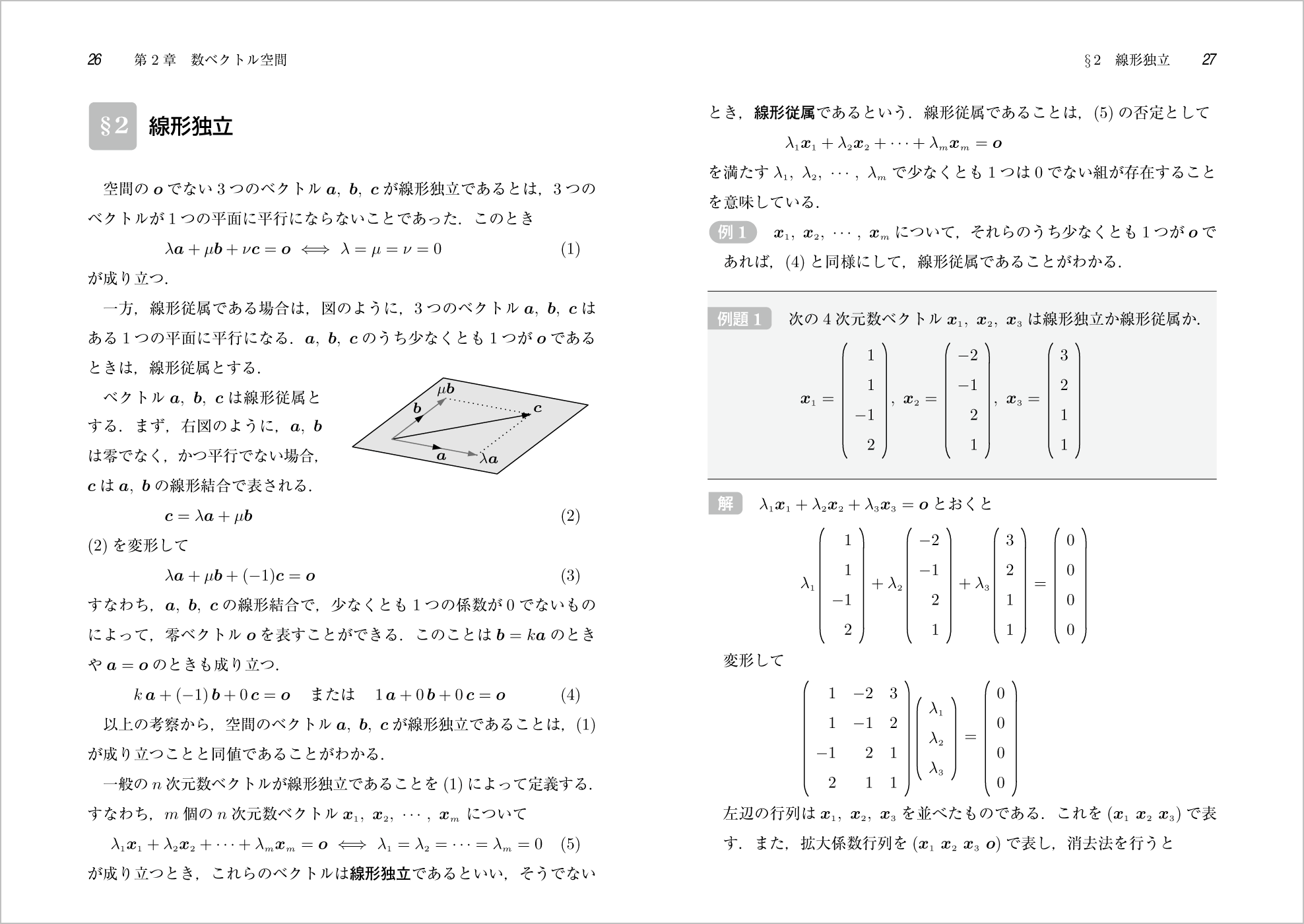
ポイント
新線形代数では２次元（平面）と３次元（空間）の幾何ベクトルを学習してきました。ここでは，４次元の数ベクトルで抽象的な数ベクトル空間を理解していきます。線形独立の概念を２次元３次元から拡張して，重要な基底の概念を身につけていきます。

４章　部分空間

ポイント
４次元数ベクトル空間の簡単な部分空間に関する例題です。基底や次元は部分空間のイメージをとらえる重要な情報です。和空間などの簡単な部分空間も先に学習して，そのあとで核や像などの抽象的な部分空間を身につけます。

５章　いろいろなベクトル空間

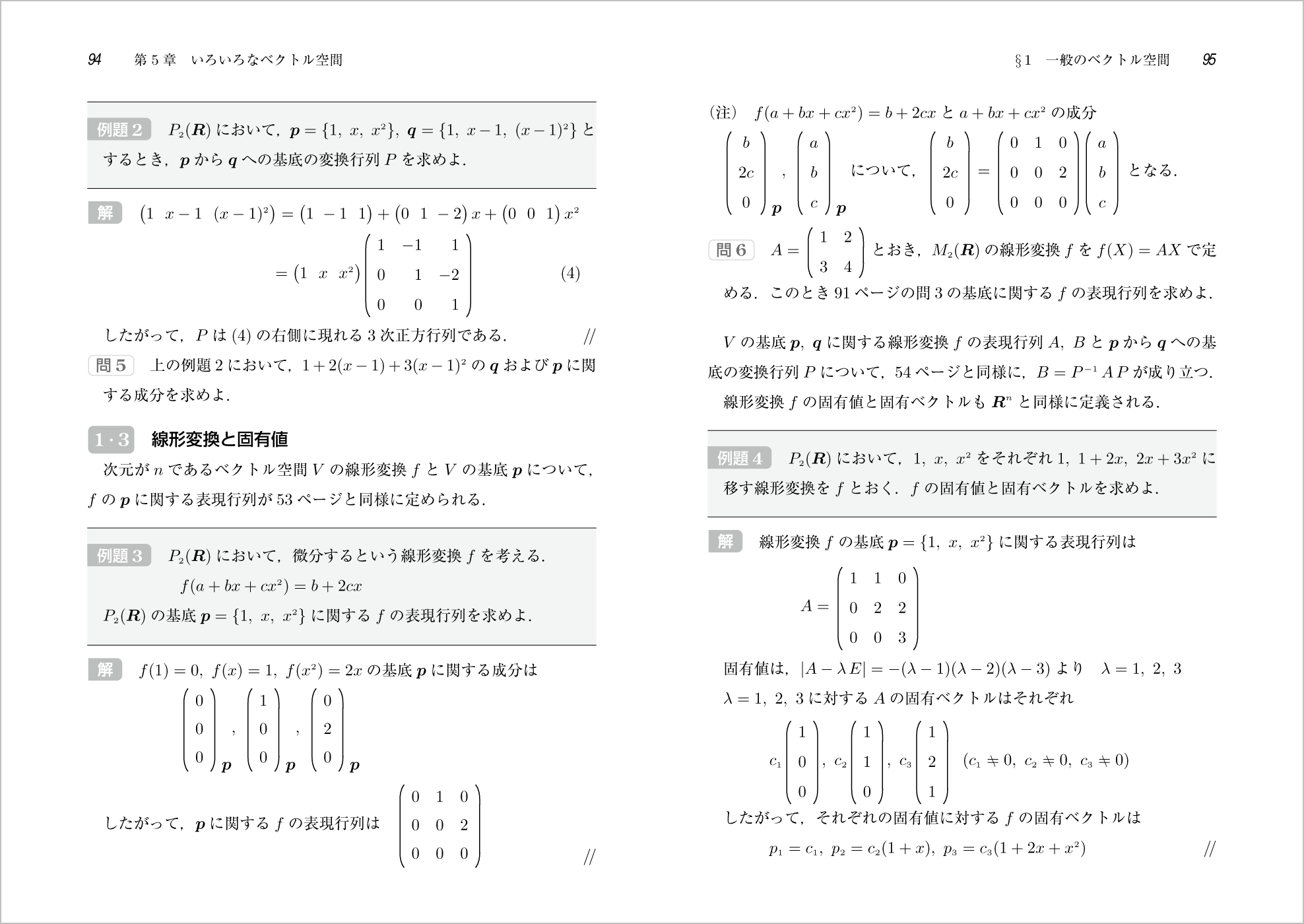
ポイント①
ここでは違ったものをベクトルととらえることによって，別世界のベクトル空間や線形変換があることを学習していきます。
ポイント②
身近な例として $x$ の２次以下の多項式をベクトルとみなして，いくつかの線形変換について考えていきます。

大学と高専のギャップになっている「ベクトル空間」

「ベクトル空間」は多くの理工系大学において線形代数の授業で教えられていて，大学編入学試験でも出題されることのある内容です。本書は，たんなる編入対策としてではなく，「ベクトル空間」をしっかりと身につけてもらうことを目的としています。
なお，編入対策の演習書としては「大学編入のための数学問題集」を用意しております。その中で「ベクトル空間」を取り扱っていますので，こちらもぜひご活用下さい。