高専・大学数学 新 微分積分Ⅰ 改訂版


新 微分積分Ⅰ
-

新 微分積分Ⅰ 改訂版 教科書 改訂版
-

新 微分積分Ⅰ 問題集 改訂版 問題集 改訂版
新 微分積分Ⅰ 改訂版
| 監修 | ||||||
|---|---|---|---|---|---|---|
| 監修 | 高遠節夫(元東邦大学教授) |
|||||
| 執筆 | ||||||
| 執筆 | 赤池祐次(呉工業高等専門学校教授) |
阿部孝之(木更津工業高等専門学校准教授) |
中川英則(小山工業高等専門学校教授) |
|||
濵口直樹(長野工業高等専門学校教授) |
松宮篤(明石工業高等専門学校教授) |
山下哲(木更津工業高等専門学校教授) |
||||
| 校閲 | ||||||
| 校閲 | 碓氷久(群馬工業高等専門学校教授) |
岡中正三(呉工業高等専門学校名誉教授) |
蔵岡誉司(東京情報⼤学総合情報学部教授) |
佐藤宏平(小山工業高等専門学校准教授) |
下田泰史(仙台高等専門学校広瀬キャンパス准教授) |
鈴木正樹(沼津工業高等専門学校教授) |
拜田稔(鹿児島工業高等専門学校教授) |
松尾幸二(一関工業高等専門学校名誉教授) |
南貴之(香川高等専門学校詫間キャンパス教授) |
横谷正明(津山工業高等専門学校教授) |
吉村弥子(神戸市立工業高等専門学校教授) |
「新 微分積分Ⅰ 改訂版」のねらい
「新微分積分Ⅰ改訂版」は,微分法,微分の応用,積分法,積分の応用の4章から成り,微分法と積分法についての基礎的事項を一通り学ぶことを目的としています。
微分法は各点ごとの関数の変化の割合に着目し,積分法は区間全体での関数の値を見るというように,両者の手法は異なり,別々に発展してきましたが,17世紀後半にニュートンやライプニッツによって両者は密接に関連づけられて,微分積分学という1つの学問に統一されたのです。現代においても,工学や自然科学に現れる現象を解析するための重要な道具となっています。
微分積分学を学び,その方法に習熟し,応用できる力を養うことは, 工学や自然科学を目指す学生にとってはとりわけ欠かすことができない事柄です。さらには,本書で学ぶことを通じて,長い時間をかけて発展してきた微分積分学という学問の興味深い内容を理解する一助になってほしいとも願っています。
- 学生が苦手とするところには説明に十分配慮をしながら,内容をコンパクトにまとめて,授業で扱いやすい構成にしています。
- 2色刷を活かしながらわかりやすい図を多く取り入れ,各章には章の内容に関連する章扉やコラムなどを設けました。
- 本文の問や練習問題の数値を見直して刷新しました。
| 目次 | 1章 微分法関数の極限と導関数/いろいろな関数の導関数 |
|---|---|
2章 微分の応用関数の変動/いろいろな応用 |
|
3章 積分法不定積分と定積分/積分の計算 |
|
4章 積分の応用面積・曲線の長さ・体積/いろいろな応用 |
-
ページ紹介①巻頭「これまで学んだ関数の復習」
-
べき関数,三角関数,指数関数,対数関数などは微分積分を学習する際にもよく出てきます。これらの関数については基礎数学で学習していますが,忘れている学生も少なくありません。
そこで本書では1章1節の冒頭で,こうした関数について簡単に復習できるページを設けています。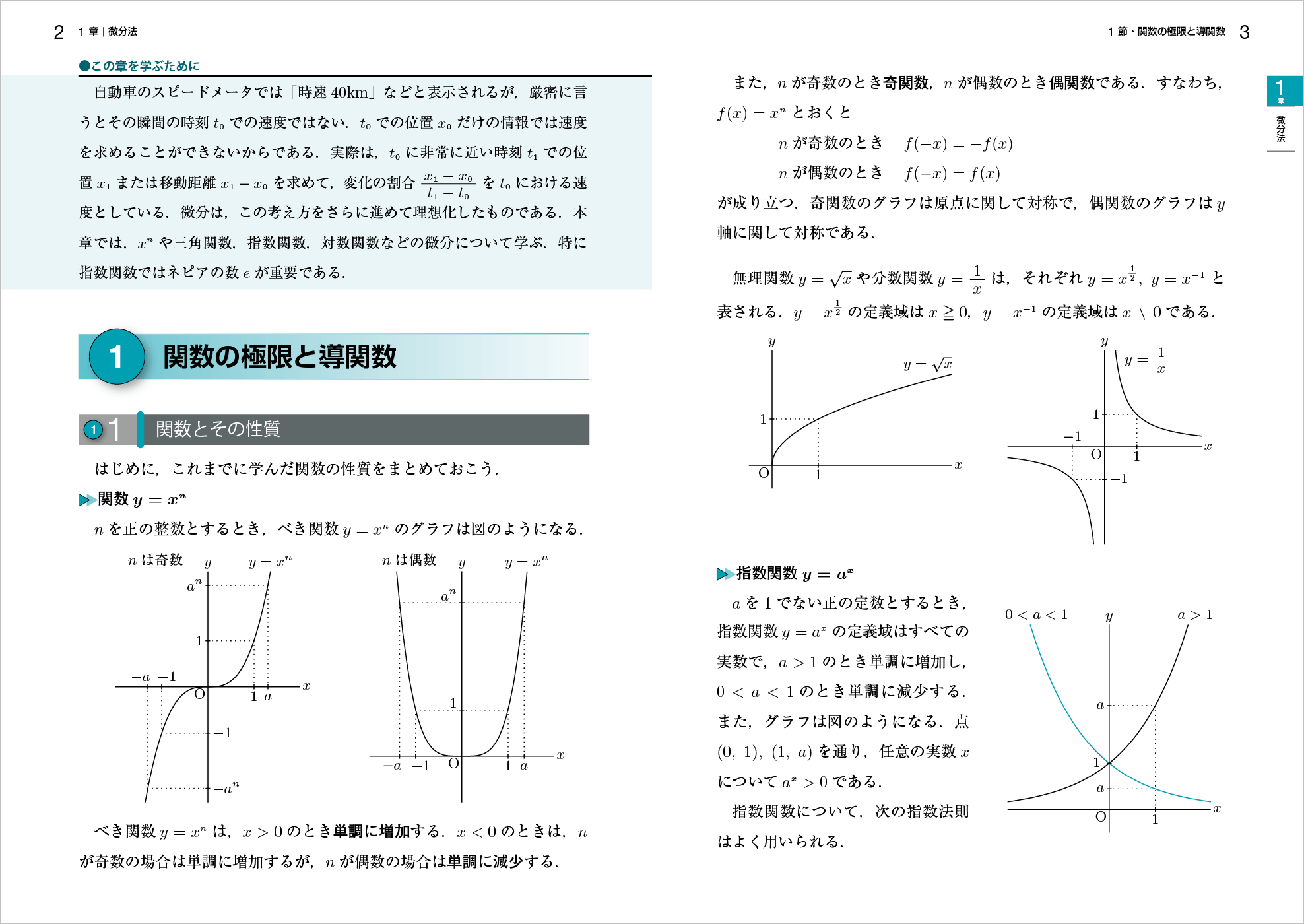
ポイント 基礎数学で学習した関数を復習できるまとめです。復習に時間がかかりそうな場合は,適宜参照するなどしてご活用ください。
ポイントをかくす
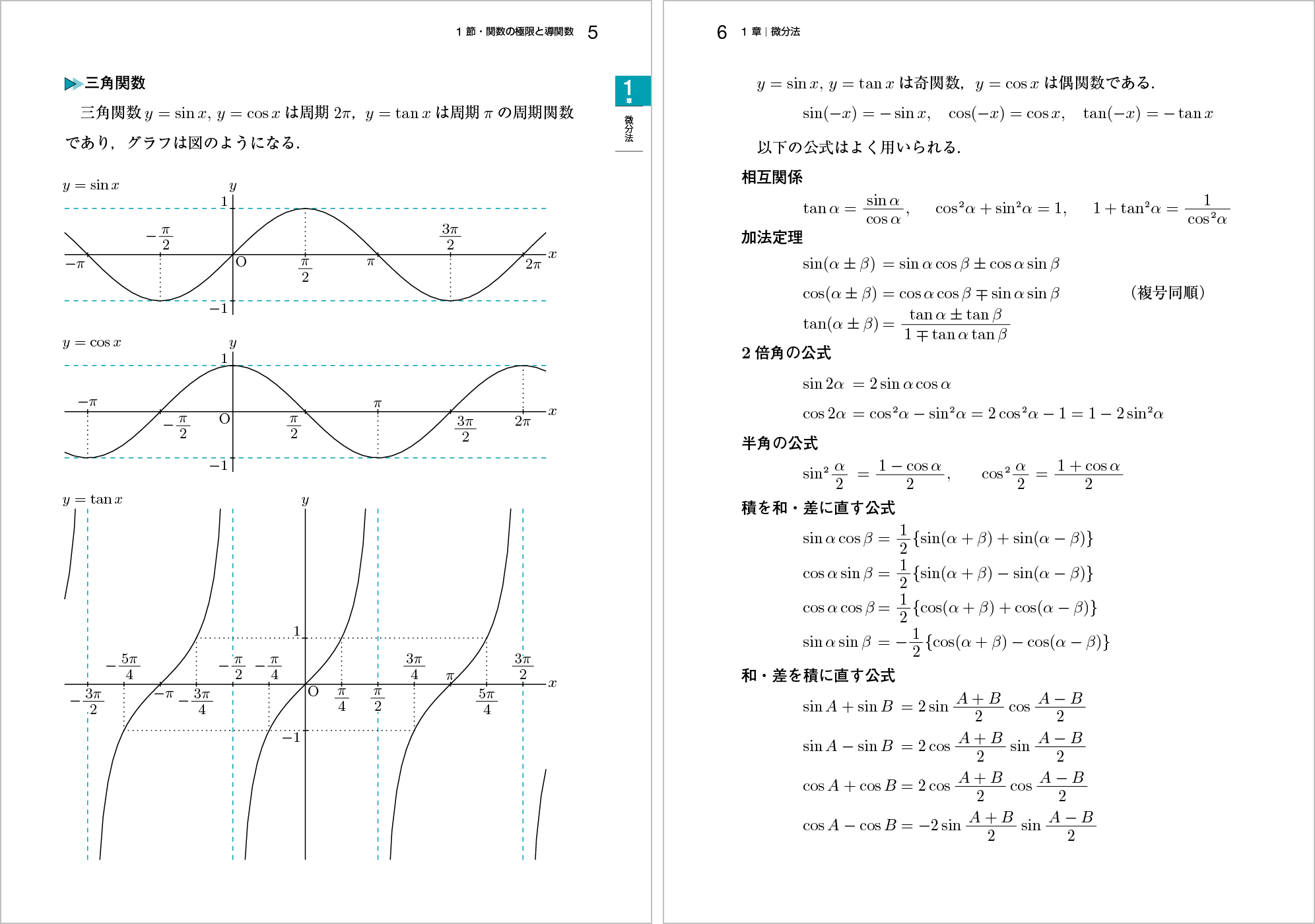
ポイント 微分積分の学習に必要な三角関数の公式をまとめました。振り返る時にも便利です。
ポイントをかくす
-
ページ紹介②導関数の定義式
-
微分係数の定義との関連で,導関数の定義式では次の3つの式を提示しています。
$f'(x) =\displaystyle \lim_{z \to x} \frac{f(z)-f(x)}{z-x} =\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} =\lim_{\varDelta x\to 0} \frac{f(x+\varDelta x)-f(x)}{\varDelta x}$2番目や3番目の式は従来通り扱ってきた式ですが,今回1番目の式を新たに取り入れました。2番目や3番目の定義式では,$x+h$ や $x+\varDelta x$ を $f$ の式に代入することになりますが,式の代入や展開などがスムーズにいかないことがあります。そのような場合1番目の式も有効です。これを使うことで説明や計算が簡単になるところがあり,定義のつまずきを軽減できます。

ポイント 式(1)の文字$z$は,以前は$X$を用いていましたが,$x$と書き分けづらいことに配慮して変更したものです。
ポイントをかくす
-
ページ紹介③旧版の1章2・2「対数関数の導関数」の見直し
-
旧版の1章2・2「対数関数の導関数」の内容について大幅に見直しました。
対数関数の導関数については,1・7「指数関数と対数関数の導関数」に移動して,合成関数の微分法によらずに指数関数の導関数と合わせて説明するようにしました。
一方,2・3は新たに「逆関数の導関数」として,埋もれていた逆関数の導関数の内容を独立させました。また2・4の「逆三角関数とその導関数」は合成関数の微分法で説明していましたが,今回は逆関数の微分法による説明に変更しています。
ポイント① 指数関数と対数関数の導関数を,一緒に扱うようにしました。
ポイント② 以前,指数関数の導関数と一緒に扱っていた「ネピアの数の性質」は,内容を独立させて1・8で扱っています。
ポイントをかくす

ポイント 逆関数の導関数の内容を,例や問いを設けてきちんと扱うようにしました。
ポイントをかくす
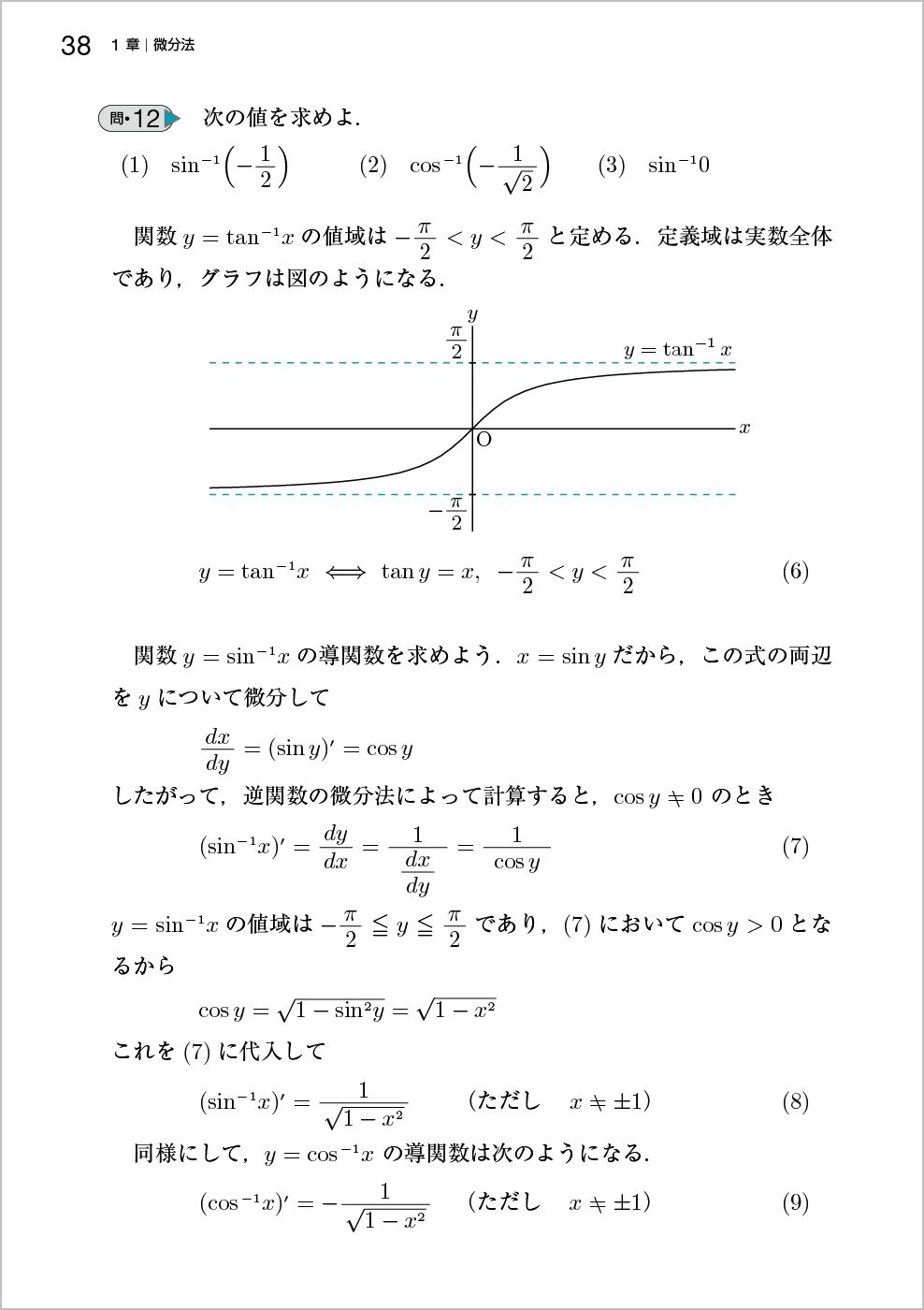
ポイント 「逆三角関数とその導関数」は合成関数の微分法で説明していましたが,今回は逆関数の微分法による説明に変更しています。
ポイントをかくす
-
ページ紹介④合成関数の微分法
-
合成関数の微分法の公式では,これまでの説明や提示の仕方を変えて,
$$\displaystyle \frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}=f'(u)g'(x)=f'\bigl(g(x)\bigr)g'(x) ~~\ \text{から}~~\ \displaystyle\frac{dy}{dx}=\frac{du}{dx}\frac{dy}{du}=\frac{dy}{du}\frac{du}{dx}$$のように入れ替えた2つの式を提示しました。
p.20の例題10で証明した公式とつながる展開にして,合成関数の微分をよりわかりやく柔軟に対応できるようにしています。
合成関数の導関数の導出における図も見直しました。
ポイント 合成関数の微分法の公式は,提示の仕方を変更しました。
ポイントをかくす

ポイント 合成関数の微分法の公式の証明では,②で紹介した導関数の定義式を利用しています。また,証明の仕方に合わせて導出の説明図も見直しました。
ポイントをかくす
-
ページ紹介⑤関数の増減の性質やロピタルの定理の配置
-
ロピタルの定理については先に慣れることを重視した構成にしています。ロピタルの定理を早めに使えるようにして,詳しい証明については章の最後で扱っています。
今回,関数の増減の性質についても同様な構成にして,その証明に必要な平均値の定理は章の最後で扱うようにしました。それにより,2章の最後の2・6「平均値の定理」で,ロルの定理,平均値の定理,関数の増減,定数関数であるための必要十分条件,コーシーの平均値の定理,ロピタルの定理の証明をまとめて扱っています。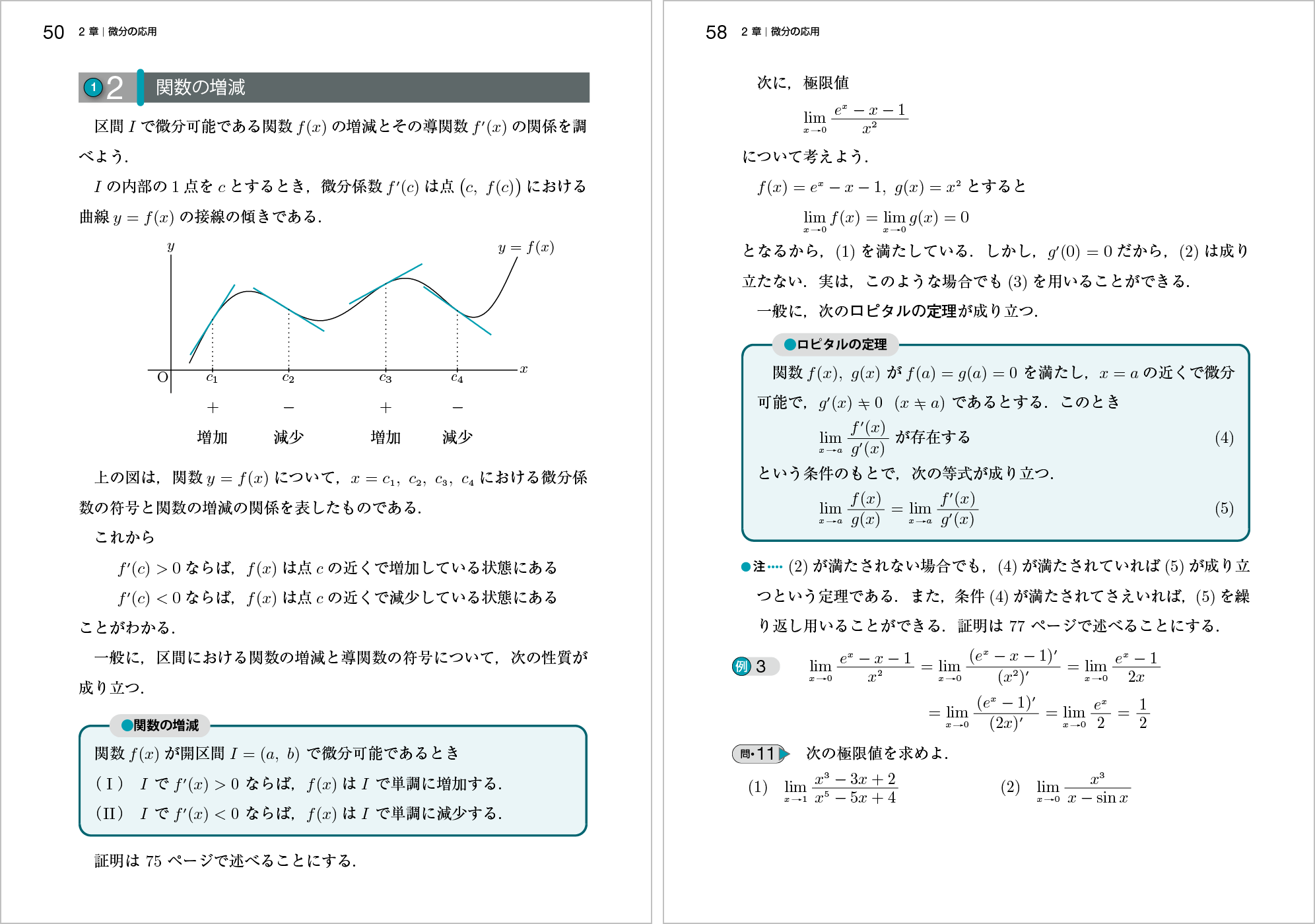
ポイント 今回,関数の増減の性質について,ロピタルの定理と同様に,詳しい証明については章の最後で扱う構成にしました。
ポイントをかくす


ポイント 「関数の増減の性質」の証明に必要な「平均値の定理」も章の最後で扱うようにしました。
それにより,2章の最後の2・6「平均値の定理」で,ロルの定理,平均値の定理,ロピタルの定理などの証明をまとめて扱っています。
ポイントをかくす
-
ページ紹介⑥積分法の導入の不定積分
-
積分の導入については,積分の意味を伝えるには定積分のほうがよくて,歴史的にもそうした流れになっていますが,区分求積法による定積分の定義は学生にとって理解しにくいところで,微分とのつながりから不定積分から入るほうが入りやすいと考えられます。
一方,不定積分の学習だけが続くと,積分の意味がわからないまま進んでしまうのも気になるところです。
本書では学生の学びやすさを考慮して,最初に不定積分の基本事項を記述し,次に定積分の意味や微分積分学の基本定理と続けて,その後で再び不定積分や定積分の公式を扱う構成にしています。
ポイント 微分を学習した直後ということで,微分の逆演算としての積分のほうが,学生にとって定着しやすいと考えられます。
ポイントをかくす
新 微分積分Ⅰ 問題集 改訂版
| 監修 | ||||
|---|---|---|---|---|
| 監修 | 高遠節夫(元東邦大学教授) |
|||
| 執筆 | ||||
| 執筆 | 赤池祐次(呉工業高等専門学校教授) |
阿部孝之(木更津工業高等専門学校准教授) |
中川英則(小山工業高等専門学校教授) |
|
濵口直樹(長野工業高等専門学校教授) |
松宮篤(明石工業高等専門学校教授) |
山下哲(木更津工業高等専門学校教授) |
||
| 校閲 | ||||
| 校閲 | 片方江(東北学院⼤学情報学部准教授) |
佐藤宏平(小山工業高等専門学校准教授) |
鈴木正樹(沼津工業高等専門学校教授) |
拜田稔(鹿児島工業高等専門学校教授) |
山岸弘幸(都立産業技術高等専門学校品川キャンパス教授) |
山中聡(津山工業高等専門学校准教授) |
横谷正明(津山工業高等専門学校教授) |
- 「新微分積分Ⅰ 改訂版」に準拠した問題集です。
- B5判のゆったりとした紙面で学習していただけます。
- 充実した基本問題(Basic)や確認問題(Check)を解くことで,教科書の内容を確実に身につけていくことができます。
- 標準問題(Step up)や発展的な内容(Plus)も豊富にとりそろえていて,学生の学力に合わせて幅広くお使いいただけます。
- 基本問題(Basic)や確認問題(Check)を中心に数値を見直して刷新しました。
| 目次 | 1章 微分法関数の極限と導関数/いろいろな関数の導関数 |
|---|---|
2章 微分の応用関数の変動/いろいろな応用 |
|
3章 積分法不定積分と定積分/積分の計算 |
|
4章 積分の応用面積・曲線の長さ・体積/いろいろな応用 |
-
ページ紹介①まとめ
-
教科書で学習した内容の要点をまとめています。

-
ページ紹介②Basic(基本問題)
-
教科書の問の定着を確認する問題です。豊富な類題で基礎・基本を身につけます。
教科書の問に対応していて,できなかった場合は右側の教科書参照ページを見て,教科書で復習することができます。
ポイント 教科書に戻って復習できるよう,対応する教科書の問いを示しました。
ポイントをかくす
-
ページ紹介③Check(確認問題)
-
Basicの定着を確認する問題です。
Checkの解答ではBasicの問題を参照しているので,Checkでできなかった問題をBasicで復習することも可能です。
ポイント Basic(基本問題)に戻って復習できるよう,対応する問題番号を示しました。
ポイントをかくす
-
ページ紹介④Step up(標準問題)
-
基礎知識を応用させて解く問題です。例題の後には関連する問題が続くように構成して,より使いやすくなりました。
ここでは大学編入試験問題も取り上げています。
ポイント① 例題と問題がセットになっている使いやすい構成です。
ポイント② Step upでは大学編入試験問題を取り上げているところがあります。
ポイント③ 余白には問題解決のためのヒントを設けています。
ポイントをかくす
-
ページ紹介⑤Plus(発展的内容と問題)
-
教科書では扱っていない発展的な内容を取り上げ,学生が自学自習で取り組むことができるようにしています。
ここでは大学編入試験問題も取り上げています。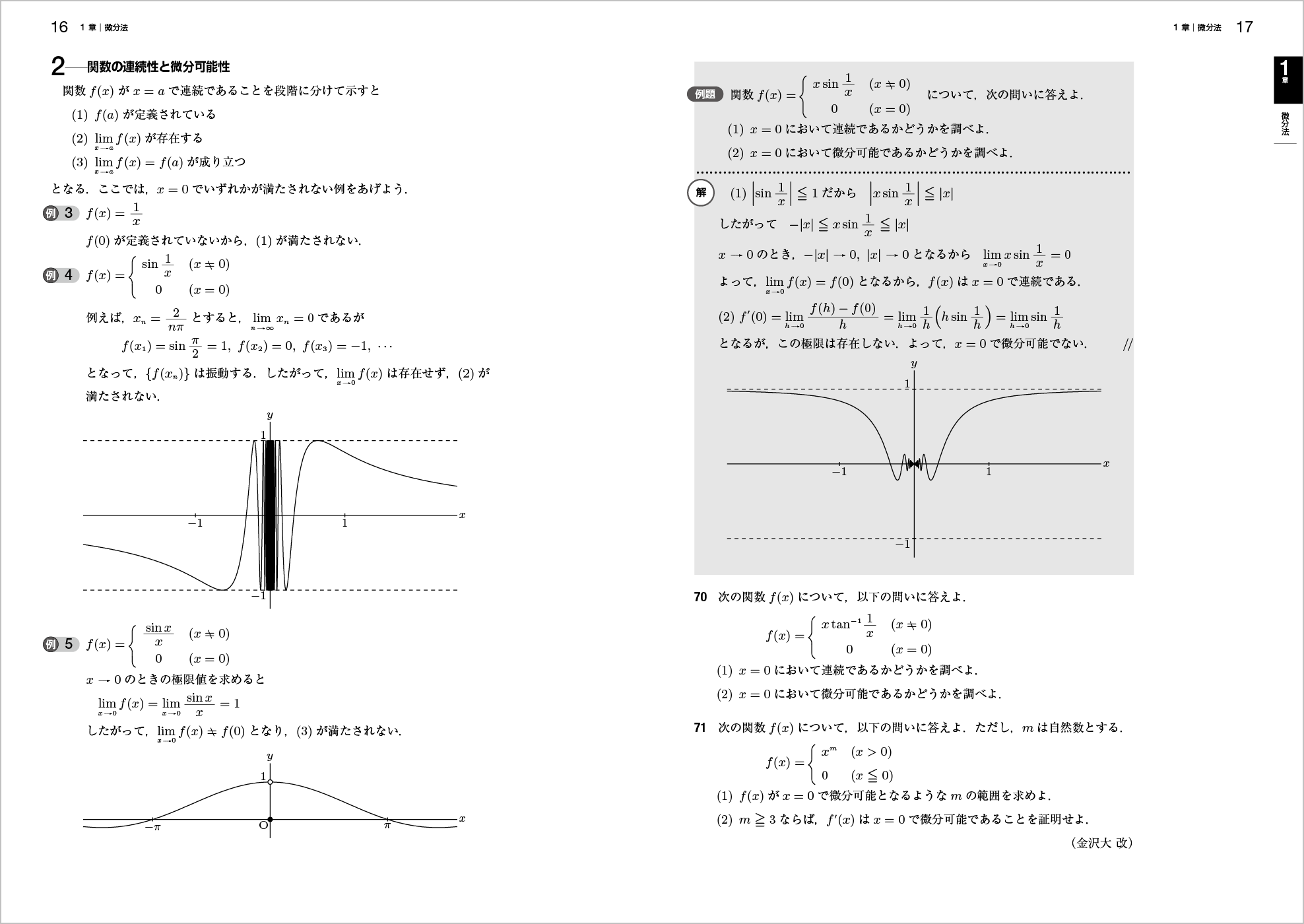
ポイント 教科書では詳しく扱っていない「関数の連続性と微分可能性」の内容を例題も取り入れながら丁寧に扱っています。
ポイントをかくす

ポイント 教科書では詳しく扱っていない「定積分の定義式の利用(区分求積法)」の内容を例題も取り入れながら丁寧に扱っています。
ポイントをかくす

ポイント 教科書では詳しく扱っていない「回転体の面積」の内容を例題も取り入れながら丁寧に扱っています。
ポイントをかくす

ポイント Plusの最後に補充問題を集めた「いろいろな問題」を設けているところもあります。
ポイントをかくす
-
ページ紹介⑥解答
-
Step upやPlusの解答には,詳しい解説をつけています。

- お届け日は地域によって異なります。
- クレジットカード、コンビニ払い、PayPay、Pay-easyが利用できます。
オンライン書店もご利用いただけます。
取扱い状況は各書店にてご確認ください。
- お届け日は地域によって異なります。
- クレジットカード、コンビニ払い、PayPay、Pay-easyが利用できます。
オンライン書店もご利用いただけます。
取扱い状況は各書店にてご確認ください。
教科書新数学シリーズ
教材・資料













































