高専・大学数学 新 確率統計 改訂版


新 確率統計
-

新 確率統計 改訂版 教科書
改訂版 -

新 確率統計 問題集 改訂版 問題集
改訂版
新 確率統計 改訂版
| 監修 | ||||
|---|---|---|---|---|
| 監修 | 高遠節夫(元東邦大学教授) |
|||
| 執筆 | ||||
| 執筆 | 阿部孝之(木更津工業高等専門学校准教授) |
碓氷久(群馬工業高等専門学校教授) |
鈴木正樹(沼津工業高等専門学校教授) |
|
西浦孝治(福島工業高等専門学校教授) |
樋口勇夫(大分工業高等専門学校教授) |
前田善文(長野工業高等専門学校名誉教授) |
||
| 校閲 | ||||
| 校閲 | 大内俊二(下関市立大学経済学部名誉教授) |
大塚隆史(北九州工業高等専門学校講師) |
田中守(都城工業高等専門学校准教授) |
冨樫瑠美(長岡工業高等専門学校准教授) |
藤崎恒晏(鹿児島工業高等専門学校名誉教授) |
宿久洋(同志社大学文化情報学部教授) |
吉村弥子(神戸市立工業高等専門学校教授) |
汪金芳(早稲⽥⼤学国際教養学部教授) |
「新 確率統計 改訂版」のねらい
新確率統計改訂版は,確率,データの整理,確率分布,推定と検定の4章から成り,確率と統計の基礎を一通り学ぶことを目的としています。また,補章を設けて,本書の学習段階としては省かざるを得なかったいろいろな検定や回帰分析などを取り上げることにしました。
確率は,その歴史こそ新しいものの,それまでは予測不可能と考えられていた未来をも科学の対象とした学問分野として,現代においては至る所で用いられています。また,実験や計測や調査などでいろいろなデータが得られますが,それらのデータを扱う際には統計の知識が必要となります。すなわち,限られたデータから全体を把握するためには,確率を基礎とした統計的な解析が不可欠です。このため,確率と統計を学び,習熟することは,工学や自然科学を目指す学生にとって欠くことのできない事柄です。さらには,本書で学ぶことを通じて,確率と統計という学問の興味深い内容に触れる一助になってほしいとも願っています。
- 学生が苦手とするところには説明に十分配慮をしながら,内容をコンパクトにまとめて,授業で扱いやすい構成にしています。
- 2色刷を活かしながらわかりやすい図を多く取り入れ,各章には章の内容に関連する章扉やコラムなどを設けました。
- 本文の問や練習問題の数値を見直して刷新しました。
| 目次 | 1章 確率確率の定義と性質/いろいろな確率 |
|---|---|
2章 データの整理1次元のデータ/2次元のデータ |
|
3章 確率分布確率変数と確率分布/統計量と標本分布 |
|
4章 推定と検定母数の推定/仮説検定 |
|
5章 補章1章の補足/2章の補足/3章の補足/4章の補足/ベイズ統計 |
-
ページ紹介①内容の厳選と補章の見直し
-
従来の内容については厳選して,授業の進度や習熟度に合わせて,足りないところを補章で適宜補充できるようにしました。 本文の該当箇所には指マークをつけて,補章のページを案内しているので,必要な場面で補章を参照することが可能です。
補章では旧版の本文や補章で扱っていた内容や説明などを取り上げています。授業の進度に合わせて補章の内容をご活用下さい。2章 データの整理

ポイント① 従来の内容を厳選してコンパクトにしているので,少ない単位数で苦労されている現場でも教えやすくなります。
ポイント② 本文の該当箇所に指マークをつけて,必要な場面で補章を参照することができます。
ポイントをかくす
補章 2章の補足
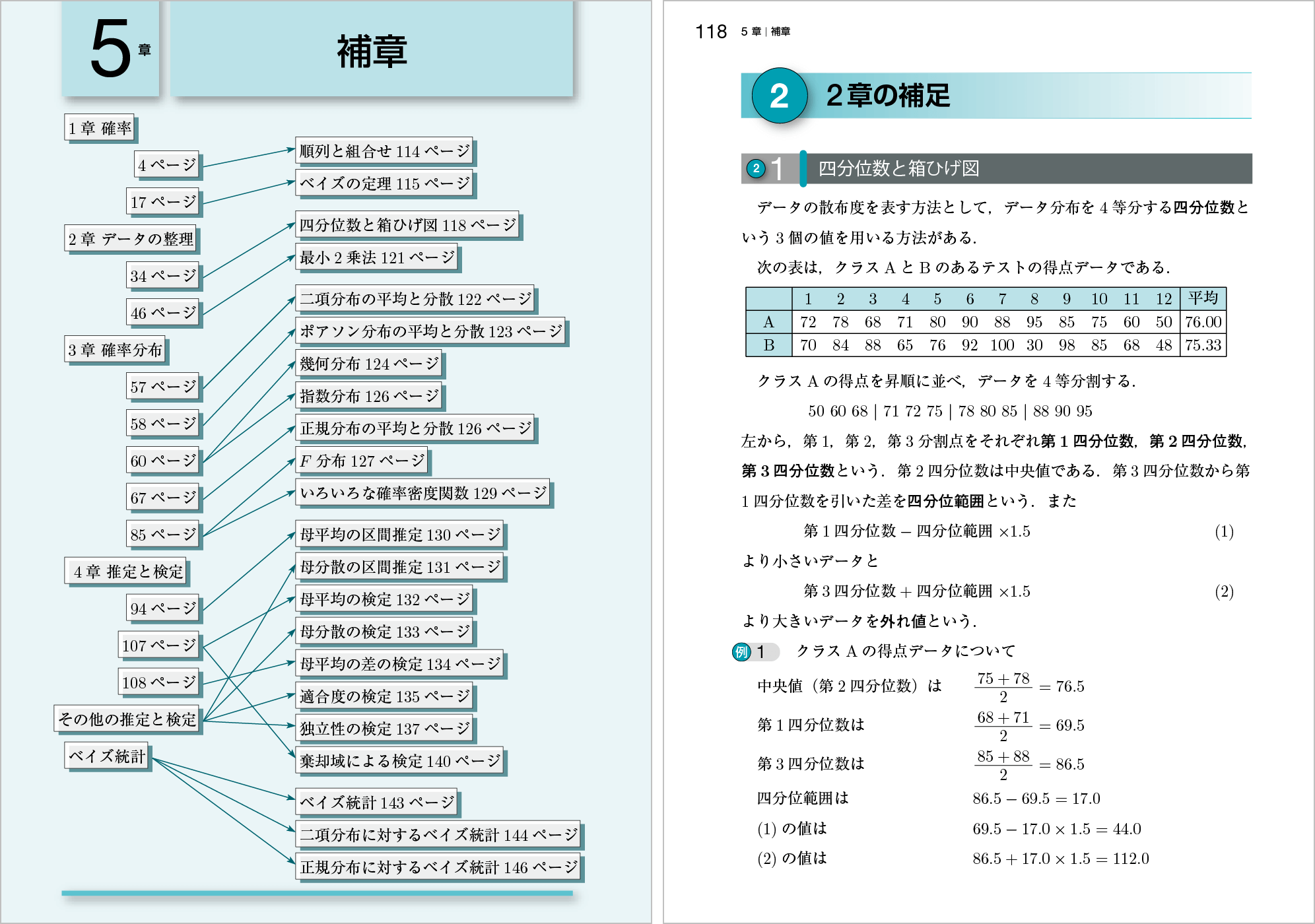
ポイント① 補章の扉では,各章の内容と補章の内容との対応関係を示しています。
ポイント② 「四分位数と箱ひげ図」は旧版の本文で扱っていましたが,中学校2年で学習する内容に変わるため,補章で扱うことにしました。復習などにご活用下さい。
ポイントをかくす
-
ページ紹介②母平均の区間推定と検定(母分散が未知の場合)
-
旧版では母平均の区間推定について,母分散が既知の場合と未知の場合を扱い,また母平均の検定でも,母分散が既知の場合と未知の場合を扱っていました。実際は母分散が未知であることが多く,新版では母分散が未知の場合,すなわちt分布を利用した推定や検定を優先して扱うことにしました。旧版で扱っていた母分散が既知の場合の母平均の区間推定は補章のp.130で,母分散が既知の場合の母平均の検定は補章のp.132に移りました。
4章 推定と検定

ポイント① 母分散が未知の場合,すなわち t 分布を利用した推定を優先して扱うことにしました。
ポイント② 母分散が既知の場合の母平均の区間推定は補章のp.130で扱っています。
ポイントをかくす

ポイント① 母分散が未知の場合,すなわちt分布を利用した検定を優先して扱うことにしました。
ポイント② 母分散が既知の場合の母平均の検定は補章のp.132で扱っています。
ポイントをかくす
補章 4章の補足

ポイント① 旧版の本文で扱っていた母分散が既知の場合の母平均の区間推定の内容です。授業の進度に合わせてご活用下さい。
ポイント② 旧版の本文で扱っていた母分散が既知の場合の母平均の検定の内容です。授業の進度に合わせてご活用下さい。
ポイントをかくす
-
ページ紹介③母平均の差の検定にウェルチの t 検定の導入
-
旧版では母平均の差の検定として,母分散が既知で正規分布を用いた検定を説明していました。母分散が未知でt分布を用いた検定についても触れていて,これは等分散であることが受容される場合なので,そのために等分散の検定(F検定)の説明も設けていました。ところがこの方法の場合,F検定はわかりにくいところであり,また2段階の検定となって誤差が想定されるため,新版では実用的なウェルチのt検定を使った説明に変更しています。
補章のp.134では,母分散が既知で正規分布を用いた検定について説明するとともに,標本の大きさが十分大きい場合についても説明しています。4章 推定と検定

ポイント① 母分散は未知であることが多く,実用的なウェルチの t 検定を使った説明に変更しました。
ポイント② 母分散が既知で,標本の大きさが十分大きい場合の母平均の差の検定は補章のp.134で扱っています。
ポイントをかくす
補章 4章の補足
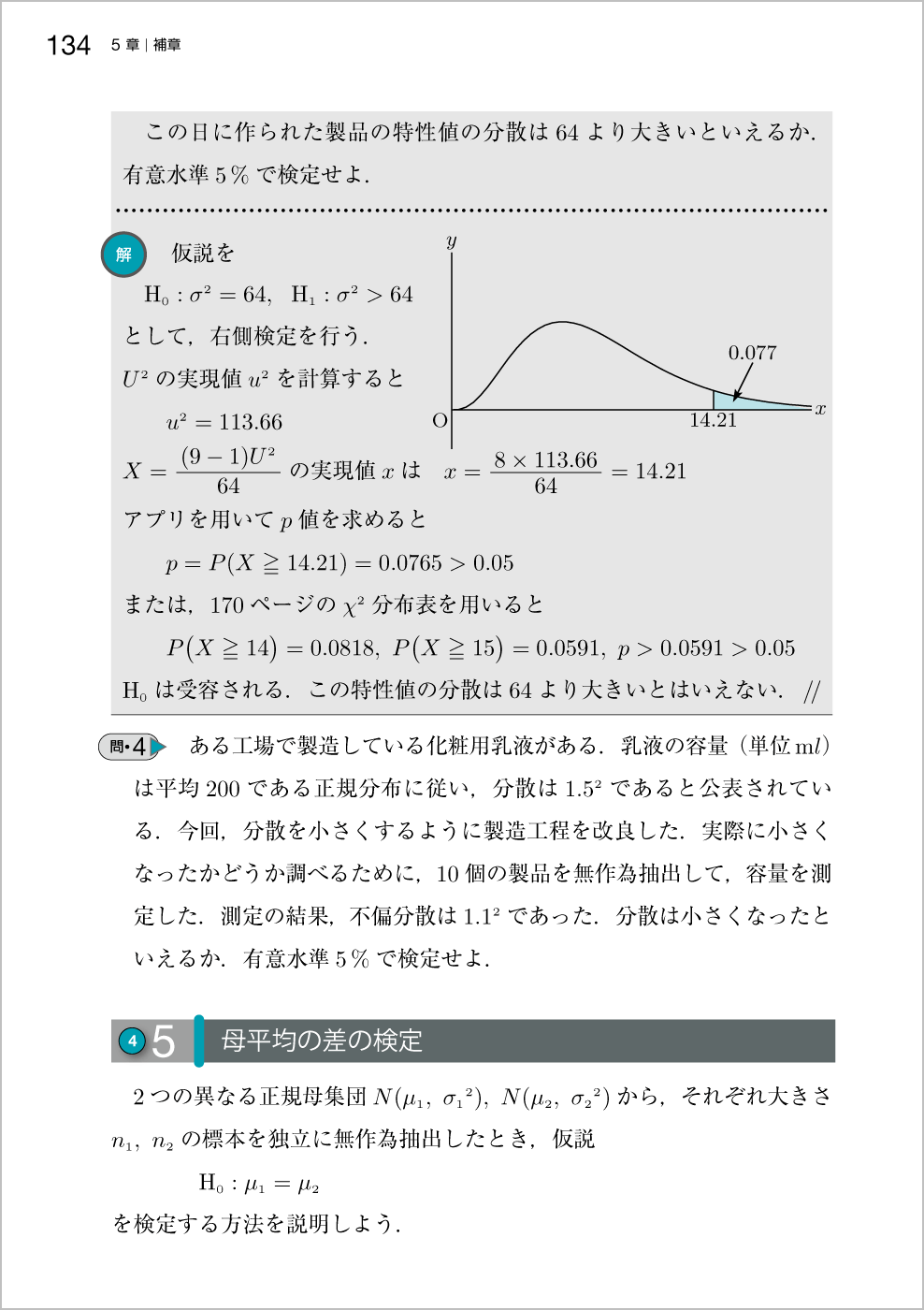
ポイント 旧版の本文で扱っていた母分散が既知で,標本の大きさが十分大きい場合の母平均の差の検定の内容です。授業の進度に合わせてご活用下さい。
ポイントをかくす
-
ページ紹介④仮説検定における p 値の導入とアプリや分布表の活用
-
仮説検定において,帰無仮説が正しいと仮定した場合に事象が起こる確率を p 値といいます。新版では仮説検定について p 値を用いた方法で説明して,p 値を計算するアプリも弊社のホームページに用意しました。一方,従来の分布表を用いた方法にも対応できるようにしています。
▶︎新確率統計改訂版WEB Contents
例題や問の解答では,アプリを使った場合と分布表を使った場合と両方で説明しました。アプリや分布表の使い方は,p.166,167で紹介しています。
なお,従来扱ってきた棄却域による検定については,補章のp.140で取り上げています。4章 推定と検定
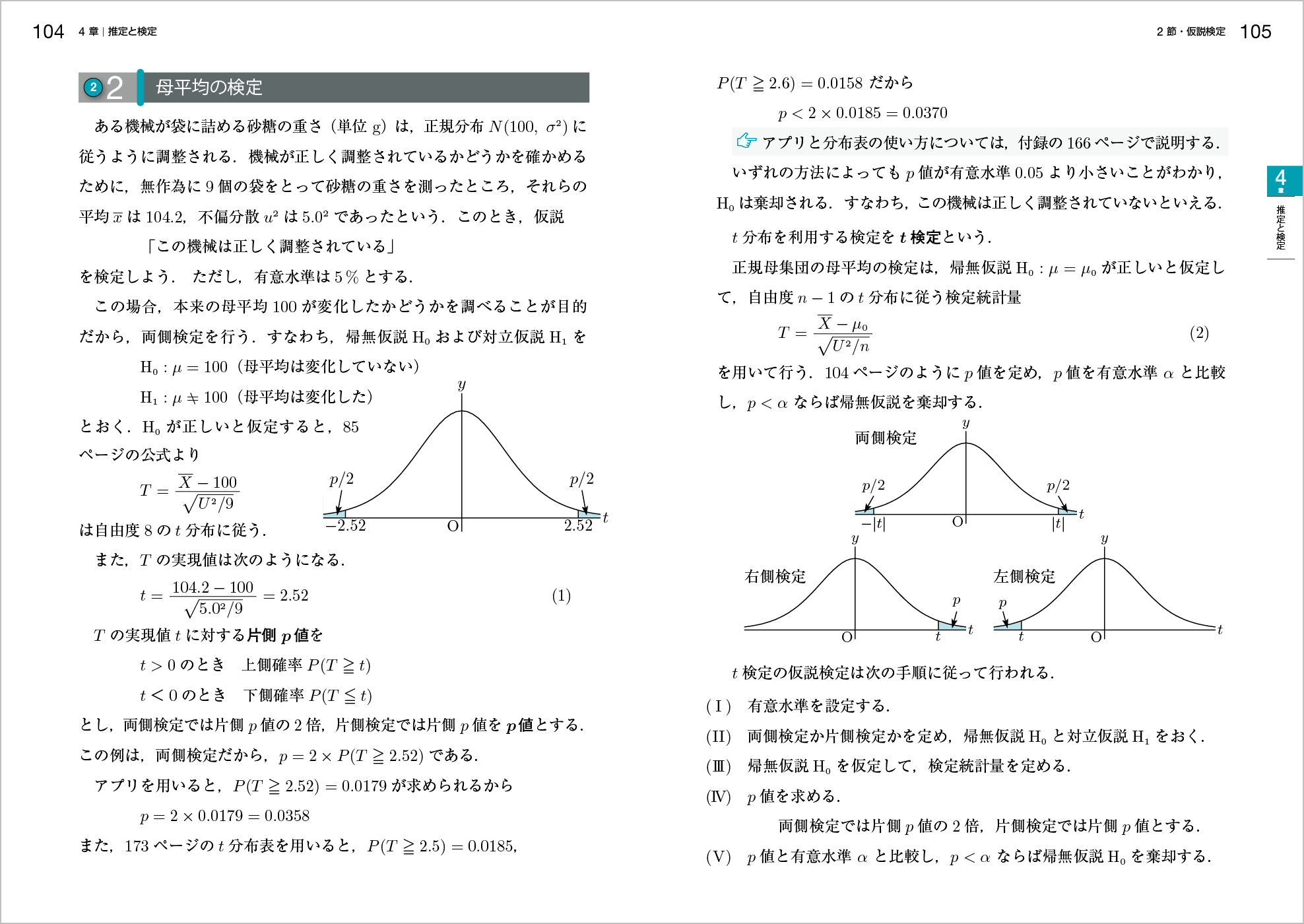
ポイント 仮説検定について p 値を用いた方法で説明するとともに,従来の分布表を用いた方法でも対応できるようにしました。アプリや分布表の使い方は,p.166,167で紹介しています。
ポイントをかくす

ポイント① 例題や問の解答では,アプリを使った場合と分布表を使った場合と両方で説明しました。
ポイント② 棄却域による検定については,補章のp.140で扱っています。
ポイントをかくす
補章 4章の補足

ポイント 旧版の本文で扱っていた棄却域による検定の内容も紹介しています。
ポイントをかくす
付録

ポイント① 分布アプリの使い方の説明です。p 値を計算するアプリも弊社のホームページに用意しました。
ポイント② 分布表の使い方の説明です。巻末に付表として用意しています。
ポイントをかくす
-
ページ紹介⑤ベイズの定理とベイズ統計
-
ベイズ統計学はデータサイエンスの有力な手法で,マーケティングにおける消費者行動の分析などに用いられています。また,機械学習との親和性も指摘されている手法です。そのベイズ統計学を支えているのがベイズの定理です。
ベイズの定理については補章のp.115で扱っています。また,ベイズ統計については,補章のp.143で扱っています。補章 1章の補足

ポイント ベイズの定理については旧版で本文で扱っていましたが,補章のp.115に移りました。授業の進度に合わせてご活用下さい。
ポイントをかくす
補章 ベイズ統計

ポイント ベイズ統計は近年様々な分野で応用されるようになり,注目を集めています。。
ポイントをかくす
-
ページ紹介⑥分布表の変更
-
正規分布表については,他の分布表に合わせて従来の分布関数の値でなく,上側確率P(Z≧z)の値にしました。逆正規分布表についてもP(Z≧z)=αとなるzの値に変更しています。また,χ2分布については,上側確率と下側確率の表,t分布については上側確率の表を追加し,従来の表についてはそれぞれ逆χ2分布表,逆t分布表と呼び名を変更しました。
付録

ポイント 正規分布表は,他の分布表に合わせて値を変更しました。使い方にご注意下さい。
ポイントをかくす

ポイント t 分布表には上側確率の表を追加し,従来の表は逆 t 分布表と呼び名を変更しました。
ポイントをかくす
新 確率統計 問題集 改訂版
| 監修 | ||||
|---|---|---|---|---|
| 監修 | 高遠節夫(元東邦大学教授) |
|||
| 執筆 | ||||
| 執筆 | 碓氷久(群馬工業高等専門学校教授) |
鈴木正樹(沼津工業高等専門学校教授) |
中川英則(小山工業高等専門学校教授) |
|
西浦孝治(福島工業高等専門学校教授) |
西垣誠一(沼津工業高等専門学校名誉教授) |
樋口勇夫(大分工業高等専門学校教授) |
||
| 校閲 | ||||
| 校閲 | 大塚隆史(北九州工業高等専門学校講師) |
高木和久(高知工業高等専門学校准教授) |
松浦將國(鹿児島工業高等専門学校准教授) |
向江頼士(宮崎⼤学教育学部准教授) |
向山一男(都立産業技術高等専門学校荒川キャンパス名誉教授) |
吉村弥子(神戸市立工業高等専門学校教授) |
涌田和芳(長岡工業高等専門学校名誉教授) |
- 「新確率統計 改訂版」に準拠した問題集です。
- B5判のゆったりとした紙面で学習していただけます。
- 充実した基本問題(Basic)や確認問題(Check)を解くことで,教科書の内容を確実に身につけていくことができます。
- 標準問題(Step up)や発展的な内容(Plus)も豊富にとりそろえていて,学生の学力に合わせて幅広くお使いいただけます。
- 基本問題(Basic)や確認問題(Check)を中心に数値を見直して刷新しました。
| 目次 | 1章 確率確率の定義と性質/いろいろな確率 |
|---|---|
2章 データの整理1次元のデータ/2次元のデータ |
|
3章 確率分布確率変数と確率分布/統計量と標本分布 |
|
4章 推定と検定母数の推定/仮説検定 |
-
ページ紹介①まとめ
-
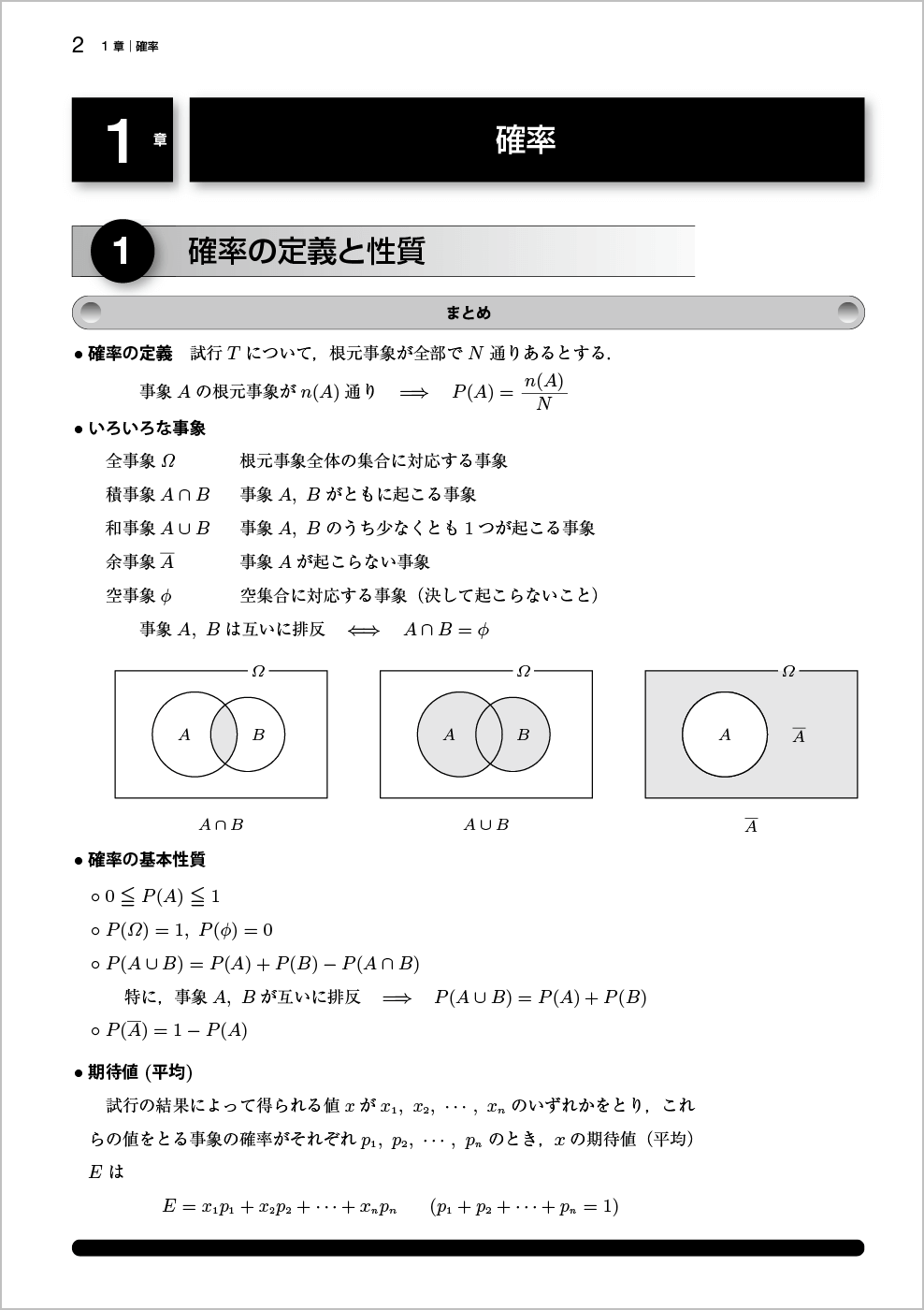
教科書で学習した内容の要点をまとめています。
1章 確率
-
ページ紹介②Basic(基本問題)
-
教科書の問の定着を確認する問題です。豊富な類題で基礎・基本を身につけます。教科書の問に対応していて,できなかった場合は右側の教科書参照ページを見て,教科書で復習することができます。
1章 確率

ポイント 教科書に戻って復習できるよう,対応する教科書の問いを示しました。
ポイントをかくす
-
ページ紹介③Check(確認問題)
-
Basicの定着を確認する問題です。
Checkの解答ではBasicの問題を参照しているので,Checkでできなかった問題をBasicで復習することも可能です。2章 データの整理

ポイント Basic(基本問題)に戻って復習できるよう,対応する問題番号を示しました。
ポイントをかくす
-
ページ紹介④Step up(標準問題)
-
基礎知識を応用させて解く問題です。例題の後には関連する問題が続くように構成して,より使いやすくなりました。
ここでは大学編入試験問題も取り上げています。3章 確率分布

ポイント① 大学編入試験問題を適宜取り上げています。
ポイント② 例題と問題がセットになっている使いやすい構成です。
ポイントをかくす
-
ページ紹介⑤Plus(発展的内容と問題)
-
教科書では扱っていない発展的な内容を取り上げ,学生が自学自習で取り組むことができるようにしています。
ここでは大学編入試験問題も取り上げました。教科書の補章に関する問題も「補章関連」のところで取り上げるようにしています。1章 確率

ポイント① 教科書の補章で扱うことになった「ベイズの定理」の内容を例題も取り入れながら丁寧に扱っています。
ポイント② Plusの最後には,補章に関連する問題を集めた「補章関連」や,その他の補充問題を集めた「いろいろな問題」を設けています。
ポイントをかくす
3章 確率分布
ポイント 教科書では詳しく扱っていない「多次元確率変数」の内容を例題も取り入れながら丁寧に扱っています。
ポイントをかくす

ポイント 教科書では詳しく扱っていない「モーメント母関数(積率母関数)」の内容を例題も取り入れながら丁寧に扱っています。
ポイントをかくす
4章 検定と推定

ポイント① 教科書の4章については内容を厳選して,一部の内容を補章に移動しました。旧版の本文で扱っていた「母平均の区間推定(母平均は既知の場合)」の内容は補章関連で取り上げています。
ポイント② 旧版の本文で扱っていた「母分散の区間推定」「母平均の検定(母分散が既知,または標本が大きい場合)」の内容は補章関連で取り上げています。
ポイントをかくす

ポイント 旧版の本文で扱っていた「母分散の検定」「母平均の差の検定(標本が大きい場合)」の内容は補章関連で取り上げています。
ポイントをかくす

ポイント 旧版の本文で扱っていた「棄却域による検定」の内容は補章関連で取り上げています。
ポイントをかくす
-
ページ紹介⑥解答
-
Step upやPlusの解答には,詳しい解説をつけています。

新 確率統計

定価:1,870円(本体1,700円+税)
体裁:A5判・上製本 / 2色 / 184頁
ISBN:978-4-477-02686-2
定価:1,870円(本体1,700円+税)
体裁:A5判・上製本 / 2色 / 184頁
ISBN:978-4-477-02686-2
| 著者 | ||||
|---|---|---|---|---|
| 著者 | 新井一道(小山工業高等専門学校名誉教授) |
市川裕子(東京工業高等専門学校教授) |
高遠節夫(東邦大学理学部訪問教授) |
|
野町俊文(都城工業高等専門学校教授) |
向山一男(都立産業技術高等専門学校名誉教授) |
村上享(松江工業高等専門学校教授) |
||
| 執筆協力 | ||||
| 執筆 協力 |
小柴俊彦(阿南工業高等専門学校名誉教授) |
|||
| 校閲 | ||||
| 校閲 | 大内俊二(下関市立大学経済学部教授) |
坪川武弘(福井工業高等専門学校名誉教授) |
八戸俊貴(一関工業高等専門学校准教授) |
藤崎恒晏(鹿児島工業高等専門学校名誉教授) |
山田康隆(北九州工業高等専門学校教授) |
涌田和芳(長岡工業高等専門学校名誉教授) |
汪金芳(横浜市立大学データサイエンス学部教授) |
「新 確率統計」のねらい
近年,統計の基本的な考えを理解するとともに,それを用いてデータを整理・分析し傾向を把握できる能力が求められるようになってきました。
工学や自然科学を学ぶ学生にとっても種々の統計の手法を学ぶことが重要になってきています。
「新確率統計」では,確率や統計の基礎となる内容を幅広く扱っていて,入門編としてお使いいただくことができます。
| 目次 | 1章 確率確率の定義と性質/いろいろな確率 |
|---|---|
2章 データの整理1次元のデータ/2次元のデータ |
|
3章 確率分布確率変数と確率分布/統計量と標本分布 |
|
4章 推定と検定母数の推定/統計的検定 |
|
5章 補章いろいろな検定/いろいろな確率分布と確率密度関数/回帰分析 |
-
ベイズの定理の取り扱い
-
近年ベイズ統計学が様々な分野で応用されるようになり,注目を集めています。そのベイズ統計学を支えているのがベイズの定理です。
ここではベイズの定理を用いる簡単な例を扱っています。1章 確率


ポイント ベイズの定理は条件つき確立の定義などから導かれます。簡単な例で定理の使い方を身につけていきます。
ポイントをかくす
-
箱ひげ図の取り扱い
-
箱ひげ図は2つ以上のデータの分布を比較する簡便な方法としてよく用いられています。高等学校では数学Iの中で四分位数に関連して取り上げられるようになりました。
データの最小値,四分位数,最大値を箱と線で表現する箱ひげ図の用い方についてここで学習していきます。2章 データの整理


ポイント 四分位はデータのちらばり具合を知るのに役立ちます。箱ひげ図は四分位を使ってちらばり具合を視覚的にとらえる方法です。
ポイントをかくす
-
連続型確率分布の導入の工夫
-
確率密度関数として
P(a≦X≦b)=∫baf(x)dxを満たす関数 f(x) を定義することがありますが,これでは「確率密度」という概念がなかなか伝わりにくい面があります。そこで前回の改訂から「確率密度」を「各区間の確率を区間幅で割ったもの」として,極限操作によって f(x) を定める方法で説明しています。新確率統計では,連続型確率分布の導入を具体的に計算できる問題にすることで,確率密度の導出過程がわかるようにしました。
3章 確率分布


ポイント 連続型確率分布の導入は,電車の待ち時間を扱いました。各区間の確率を区間幅で割って,確率密度を具体的に求めていきます。
ポイントをかくす
-
標本分布を早く学べるように
-
標本平均の平均と分散は,多次元確率変数の平均と分散の性質から得られます。
従来は標本分布を学習する前に,多次元確率変数についてしっかり説明をしてきました。しかし多次元確率変数の内容には,やや高度な内容を含むため理解するのに苦労する面もありました。
そこで新確率統計では,多次元確率変数の扱いを傍用問題集のPLUSに委ねて,無理のない形で確率変数の関数を扱って標本分布を学ぶという流れにしました。3章 確率分布


ポイント 2次元確率変数の関数の平均や分散の性質について確認していきます。従来扱ってきた同時確率密度関数や周辺確率密度関数などの概念は,問題集のPLUSで扱うことにしました。
ポイントをかくす
-
t 分布表の変更
-
従来の t 分布表は,両側検定に配慮した両側 α 点を載せていましたが,他の分布表と異なるため使う時に戸惑いを招くことがありました。そこで今回は上側 α 点を用いた分布表に変更しました。
上側 α 点:P(T≧tn(α))=α) となる tn(α) の値これにより t 分布表も他の分布表と同じように使うことができるようになりました。
付録
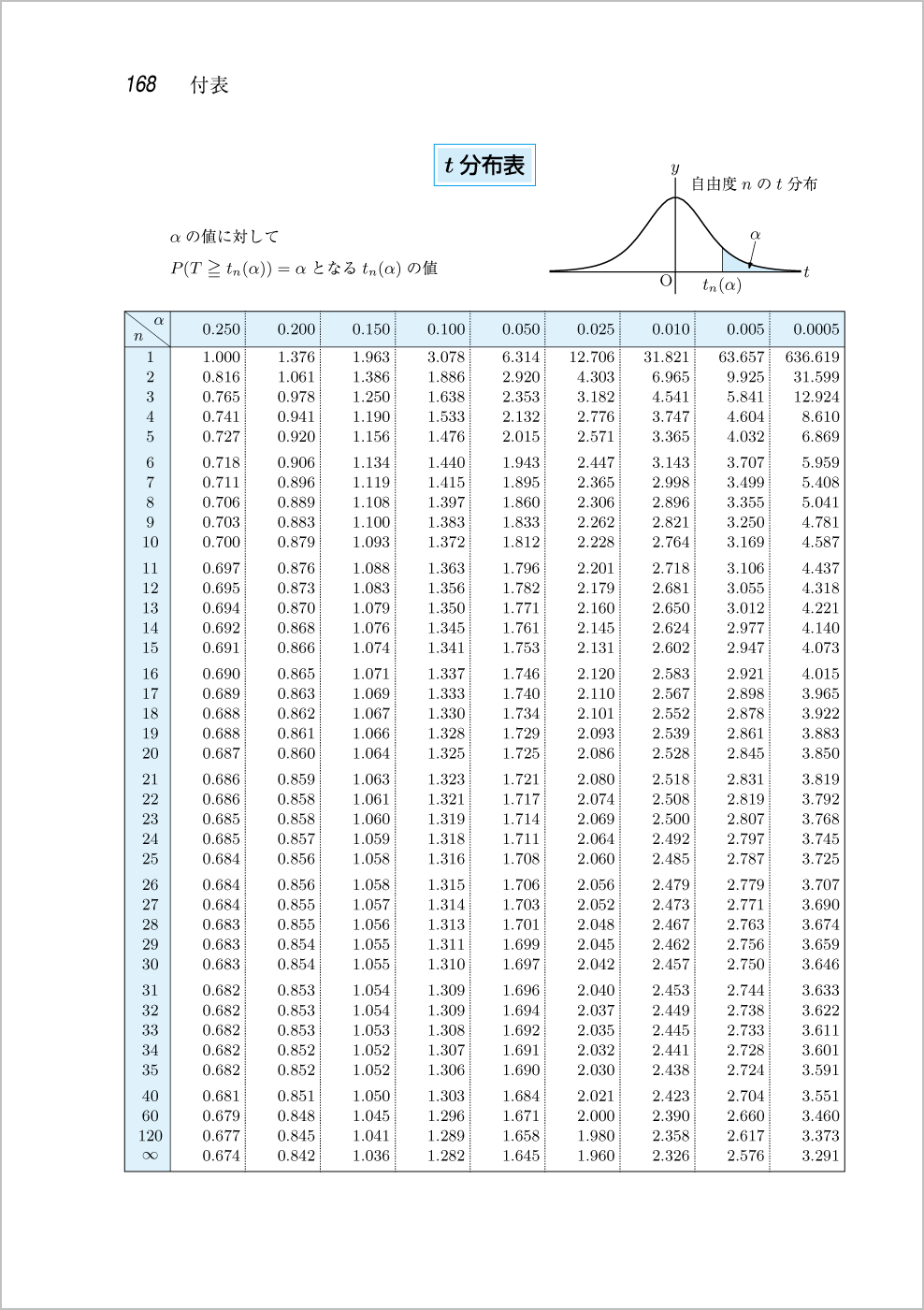

ポイント 両側 α 点から上側 α 点にすることで,他の分布表と同じように使うことができるようになりました。
ポイントをかくす
新 確率統計 問題集

定価:924(本体840円+税)
体裁:B5判 / 84頁
ISBN:978-4-477-02688-6
定価:924(本体840円+税)
体裁:B5判 / 84頁
ISBN:978-4-477-02688-6
| 著者 | ||||
|---|---|---|---|---|
| 著者 | 新井一道(小山工業高等専門学校名誉教授) |
市川裕子(東京工業高等専門学校教授) |
高遠節夫(東邦大学理学部訪問教授) |
西垣誠一(沼津工業高等専門学校名誉教授) |
野町俊文(都城工業高等専門学校教授) |
向山一男(都立産業技術高等専門学校名誉教授) |
村上享(松江工業高等専門学校教授) |
||
| 校閲 | ||||
| 校閲 | 門脇聖(松江工業高等専門学校准教授) |
藤崎恒晏(鹿児島工業高等専門学校名誉教授) |
||
山田康隆(北九州工業高等専門学校教授) |
涌田和芳(長岡工業高等専門学校名誉教授) |
「新 確率統計 問題集のねらい
「新確率統計」に準拠した問題集です。
学習内容の確実な定着を図る基本問題・確認問題,応用力をつける標準問題,課題研究「PLUS」の構成で,学力に合わせて幅広くお使いいただけます。
| 目次 | 1章 確率確率の定義と性質/いろいろな確率/PLUS |
|---|---|
2章 データの整理1次元のデータ/2次元のデータ/PLUS |
|
3章 確率分布確率変数と確率分布/統計量と標本分布/PLUS |
|
4章 推定と検定母数の推定/統計的検定/PLUS |
-
ゆったりとしたB5判サイズ
-
これまでの問題集はA5判でしたが,新シリーズではゆったりとしたB5判にしました。
ゆったりとした紙面に豊富な類題を取りそろえ,余白には教科書の参照ページを設けたりしています。1章 確率


ポイント ゆったりとした紙面にたくさんの類題を取りそろえ,BASIC(基本問題)の余白には教科書の参照ページを設けました。
ポイントをかくす
-
BASIC(基本問題)の充実
-
「BASIC」は基礎知識を身につけさせる問題です。
従来の基本問題には,もっと多くの問題を載せて欲しいという要望をいただいておりましたので,新シリーズのBASICでは,教科書の問と対応させた類題を取りそろえることで,基礎・基本の定着が図れるようにしました。
教科書の参照ページをわかりやすく示したので,対応する教科書の問に振り返るのも容易です。4章 推定と検定

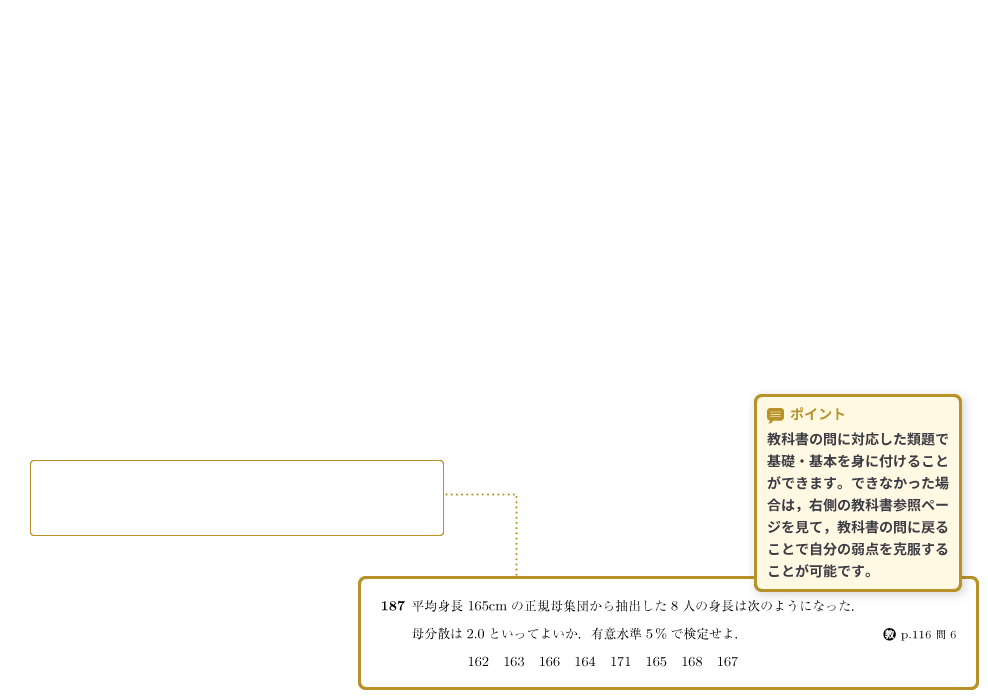
ポイント 教科書の問に対応した類題で基礎・基本を身に付けることができます。できなかった場合は,右側の教科書参照ページを見て,教科書の問に戻ることで自分の弱点を克服することが可能です。
ポイントをかくす
-
CHECK(確認問題)の新設
-
「CHECK」はBASIC(基本問題)の定着を確認する問題です。
BASICの問題の中で典型的なものを1ページにまとめています。BASICに自信のある方は,最初にCHECKからお使いいただくことも可能です。
CHECKの解答には,関連するBASICの問題番号を示しているので,できなかった問題があれば,BASICに戻って復習するのも容易です。2章 データの整理

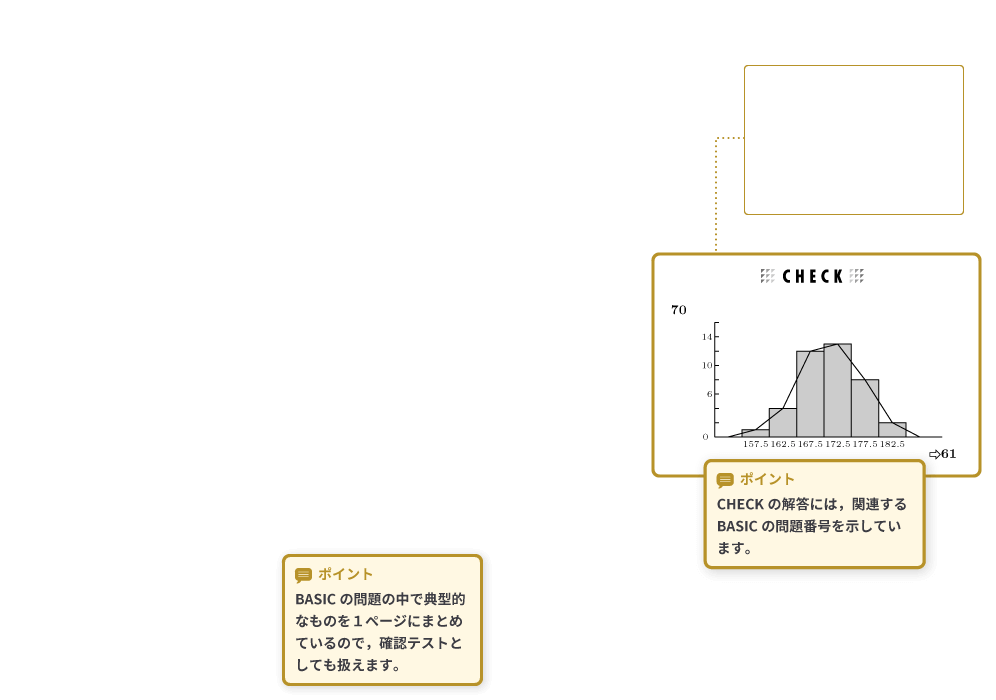
ポイント① BASICの問題の中で典型的なものを1ページにまとめているので,確認テストとしても扱えます。
ポイント② CHECKの解答には,関連するBASICの問題番号を示しています。
ポイントをかくす
-
応用力を育てるSTEP UP(標準問題)
-
「STEP UP」は,これまで学習してきた基礎知識を応用させて解く問題です。
考え方や解き方を示したほうがよいところでは,「例題」として考え方や解き方を示し,直後に例題に関連する問題を取り入れました。
ここでは大学編入試験問題も取り上げています。3章 確率分布

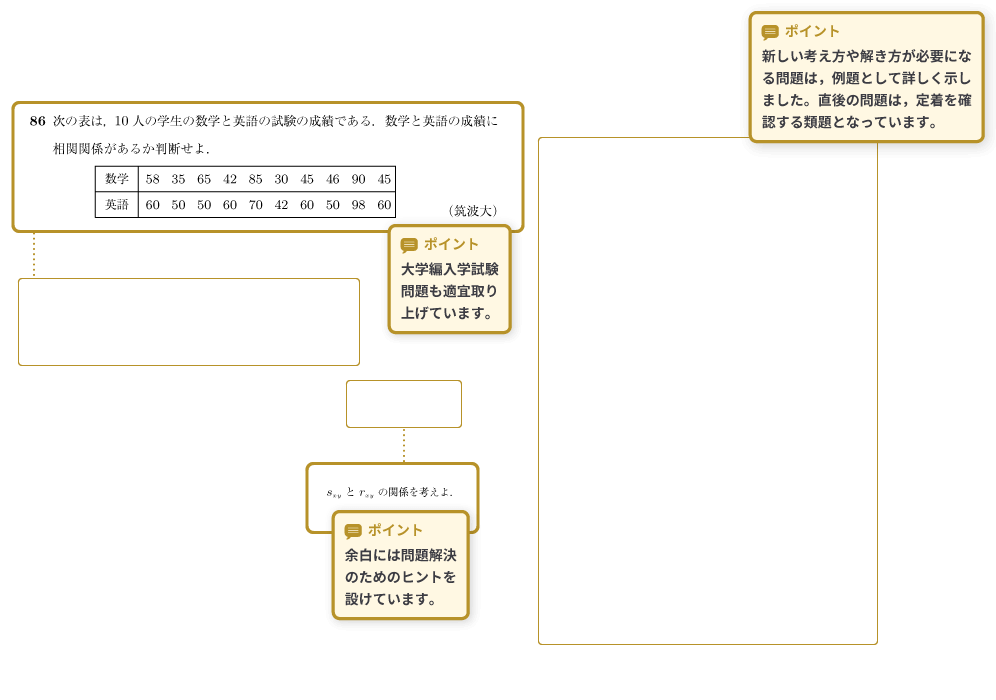
ポイント① 大学編入学試験問題も適宜取り上げています。
ポイント② 余白には問題解決のためのヒントを設けています。
ポイント③ 新しい考え方や解き方が必要になる問題は,例題として詳しく示しました。直後の問題は,定着を確認する類題となっています。
ポイントをかくす
-
発展的な内容のPLUS(課題研究)
-
「PLUS」では,教科書で以前扱っていた内容や,教科書で詳しく扱っていない発展的な内容を取り上げ,学生が自分自身で考えることができるように本文や解答を工夫しています。
ここでは大学編入試験問題も取り上げています。3章 確率分布

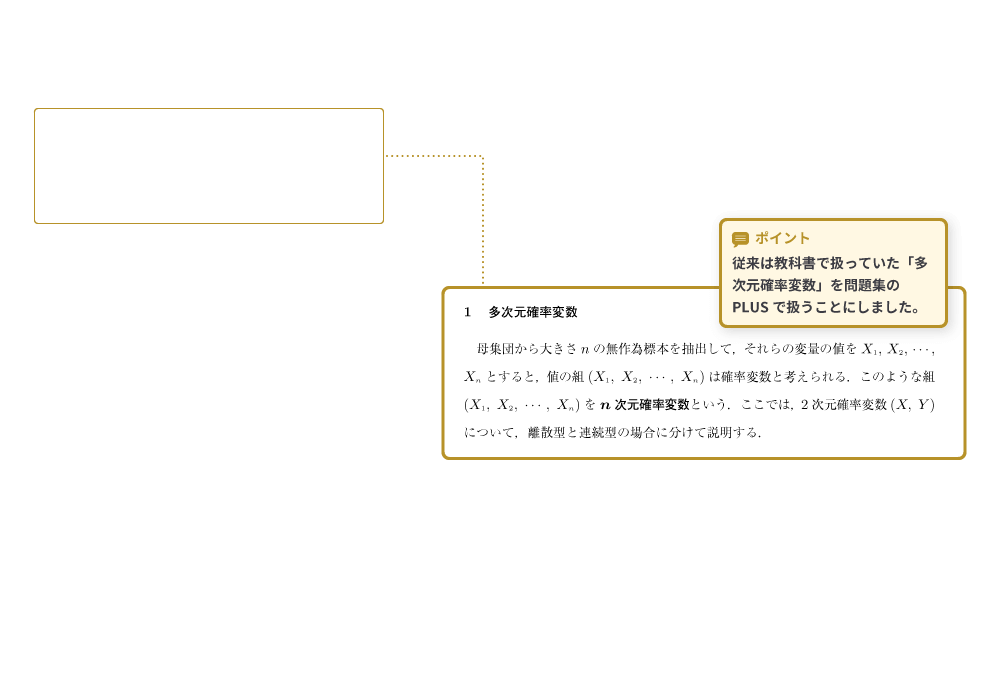
ポイント 従来は教科書で扱っていた「多次元確率変数」を問題集のPLUSで扱うことにしました。
ポイントをかくす


ポイント 教科書では扱っていない「歪度と尖度」の内容を例題も取り入れながら丁寧に扱っています。
ポイントをかくす


ポイント 教科書では扱っていない「モーメント母関数」の内容を例題も取り入れながら丁寧に扱っています。
ポイントをかくす
4章 推定と検定


ポイント 教科書では扱っていない「適合度の検定」の内容も例題を取り入れながら丁寧に扱っています。
ポイントをかくす

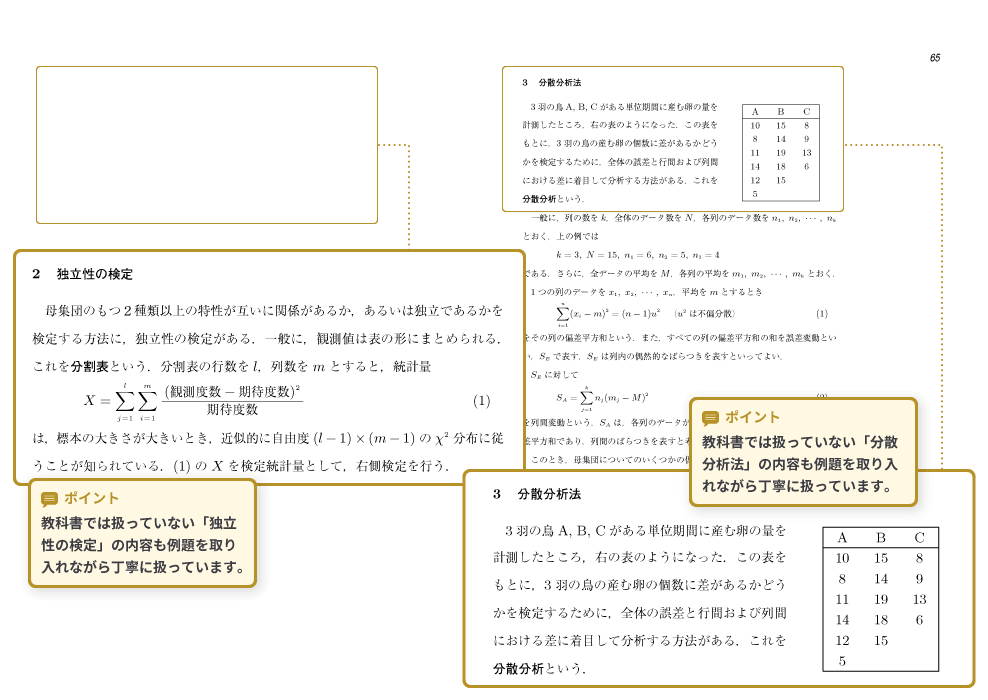
ポイント① 教科書では扱っていない「独立性の検定」の内容も例題を取り入れながら丁寧に扱っています。
ポイント② 教科書では扱っていない「分散分析法」の内容も例題を取り入れながら丁寧に扱っています。
ポイントをかくす
教科書新数学シリーズ
教材・資料










































