高専・大学数学 新 微分積分Ⅱ 改訂版


新 微分積分Ⅱ
-

新微分積分Ⅱ 改訂版 教科書
改訂版 -
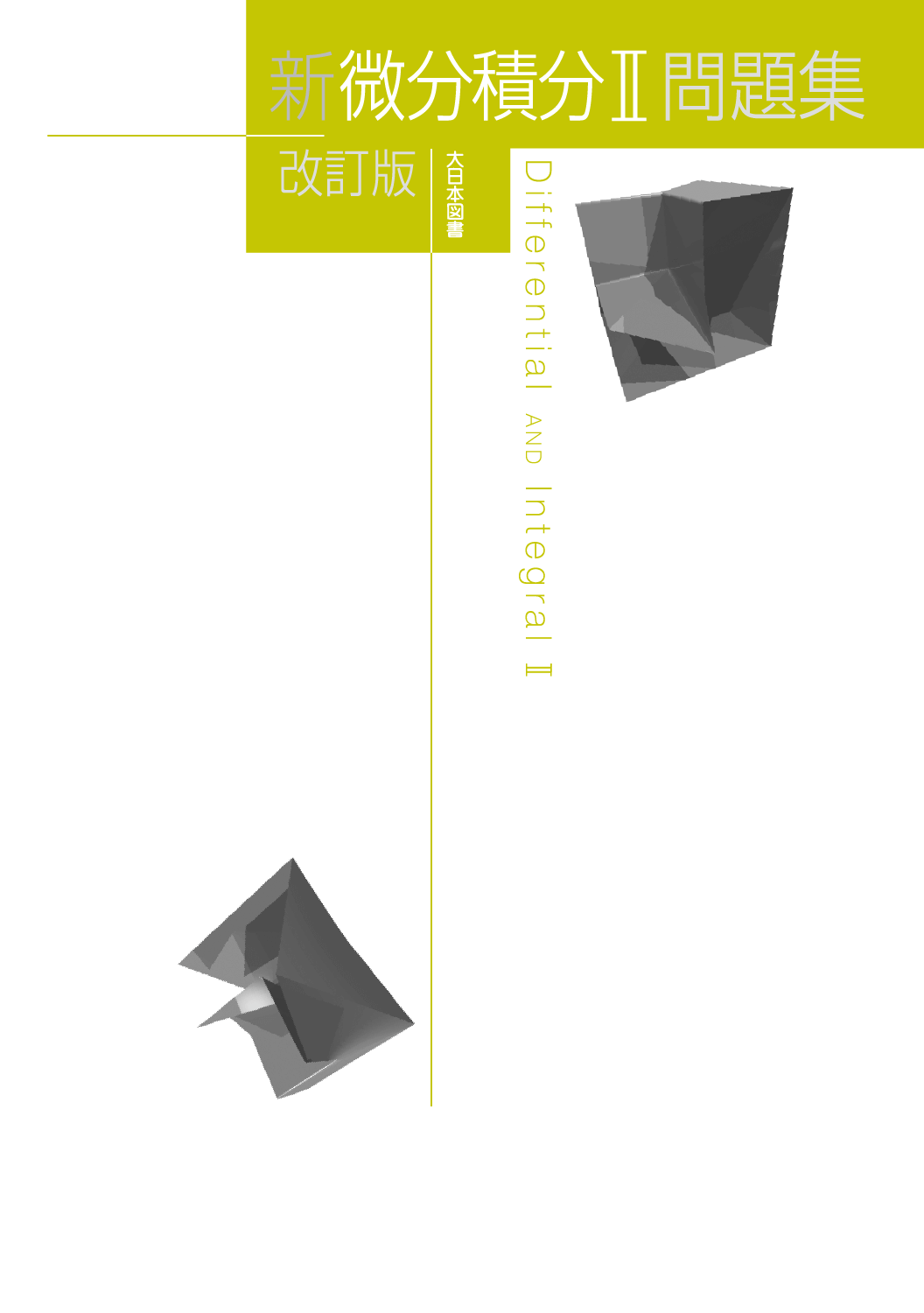
新微分積分Ⅱ 問題集 改訂版 問題集
改訂版
新 微分積分Ⅱ 改訂版
| 監修 | |||||
|---|---|---|---|---|---|
| 監修 | 高遠節夫(元東邦大学教授) |
||||
| 執筆 | |||||
| 執筆 | 小谷泰介(釧路工業高等専門学校准教授) |
篠原知子(都立産業技術高等専門学校品川キャンパス教授) |
高橋正郎(久留米工業高等専門学校准教授) |
||
拜田稔(鹿児島工業高等専門学校教授) |
濵口直樹(長野工業高等専門学校教授) |
山下哲(木更津工業高等専門学校教授) |
|||
| 校閲 | |||||
| 校閲 | 飯間圭一郎(奈良工業高等専門学校准教授) |
大澤智子(旭川工業高等専門学校教授) |
兼下英司(仙台高等専門学校広瀬キャンパス准教授) |
河原永明(茨城工業高等専門学校教授) |
齋藤純一(都立産業技術高等専門学校荒川キャンパス教授) |
佐藤宏平(小山工業高等専門学校准教授) |
西垣誠一(沼津工業高等専門学校名誉教授) |
山岸弘幸(都立産業技術高等専門学校品川キャンパス准教授) |
森田健二(石川工業高等専門学校教授) |
横谷正明(津山工業高等専門学校教授) |
「新 微分積分Ⅱ 改訂版」のねらい
新微分積分Ⅱ改訂版は,関数の展開,偏微分,重積分,微分方程式の4章から成り,微分積分の基礎を一通り学んだ後に,さらに発展的で応用的な内容を学ぶことを目的としています。
関数の展開は,関数をいわば無限個の項をもつ多項式で表すことであり,この表し方により関数の特質が的確に示され,精度の良い近似計算も可能となるものです。ただ,無限という極限操作が用いられるため,初学者にとっては理解しにくい分野でもあります。
次に,偏微分と重積分は,複数の独立変数をもつ関数の微分と積分であり,工学,自然科学に現れる多くの現象を記述し,解析するために用いられます。
また,微分方程式は,工学や自然科学に現れる現象を解析するための大切な手段です。
いずれの章でも基礎的事項の定着に重点をおき,応用的な内容を避けてわかりやすく解説しています。そこで,各章の応用的な内容については,対応箇所を明示して巻末の「補章」で解説することにしました。これらの内容を学び,その方法に習熟し,応用できる力を養うことは,工学や自然科学を目指す学生にとって欠かすことができない事柄です。
- 学生が苦手とするところには説明に十分配慮をしながら,内容をコンパクトにまとめて,授業で扱いやすい構成にしています。
- 2色刷を活かしながらわかりやすい図を多く取り入れ,各章には章の内容に関連する章扉やコラムなどを設けました。
- 本文の問や練習問題の数値を見直して刷新しました。
| 目次 | 1章 関数の展開関数の展開 |
|---|---|
2章 偏微分偏微分法/偏微分の応用 |
|
3章 重積分2重積分/変数の変換と重積分 |
|
4章 微分方程式1階微分方程式/2階微分方程式 |
|
5章 補章1章の補足/2章の補足/3章の補足/4章の補足 |
-
ページ紹介①補章の見直しと使いやすさの改善
-
旧版では1章詳説「関数の展開」を設けていましたが,いただいたご意見をもとに,補章の内容や使い方を見直しました。本文と関連のある内容や説明などを補章の中にそろえて,本文の該当箇所には指マークをつけて,補章のページを案内するようにしました。必要な場面で補章を参照することが可能です。
補章では,1章詳説「関数の展開」にあった内容や,その他の発展的な内容を取り上げたり,本文で扱っていた内容を一部移動したりしました。授業の進度に合わせて補章の内容をご活用下さい。1章 関数の展開
ポイント 補章の内容や使い方を大幅に見直しました。本文の該当箇所に指マークをつけて,必要な場面で補章を参照することができます。
ポイントをかくす
補章 1章の補足

ポイント① 補章の扉では,各章の内容と補章の内容との対応関係を示しています。
ポイント② 「マクローリンの定理と誤差の限界」は旧版の1章詳説「関数の展開」で扱っていた内容です。
ポイントをかくす
-
ページ紹介②ド・モアブルの公式とその利用
-
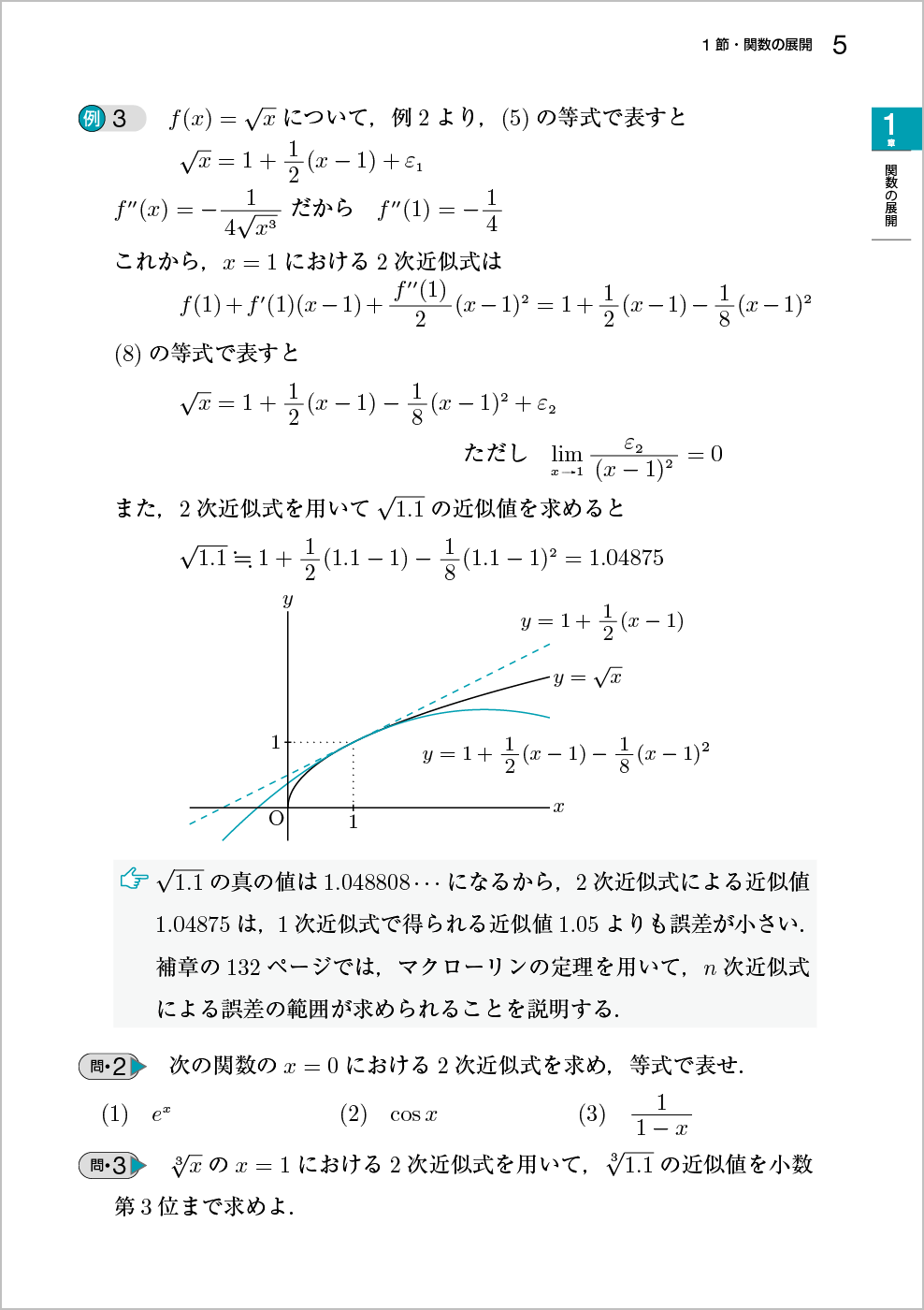
これまでド・モアブルの公式はオイラーの公式から導くだけでしたが,ド・モアブルの公式は複素数の計算で非常によく使われる式です。新版ではド・モアブルの公式の利用場面として,3倍角の公式を導く問題や複素数の$n$乗を求める問題を例題として追加して,使い方がわかるようにしました。
1章 関数の展開
ポイント ド・モアブルの公式を使って,3倍角の公式を導く問題や複素数の$n$乗を求める問題を例題として追加しました。
ポイントをかくす
-
ページ紹介③「積分の順序変更」の見直し
-
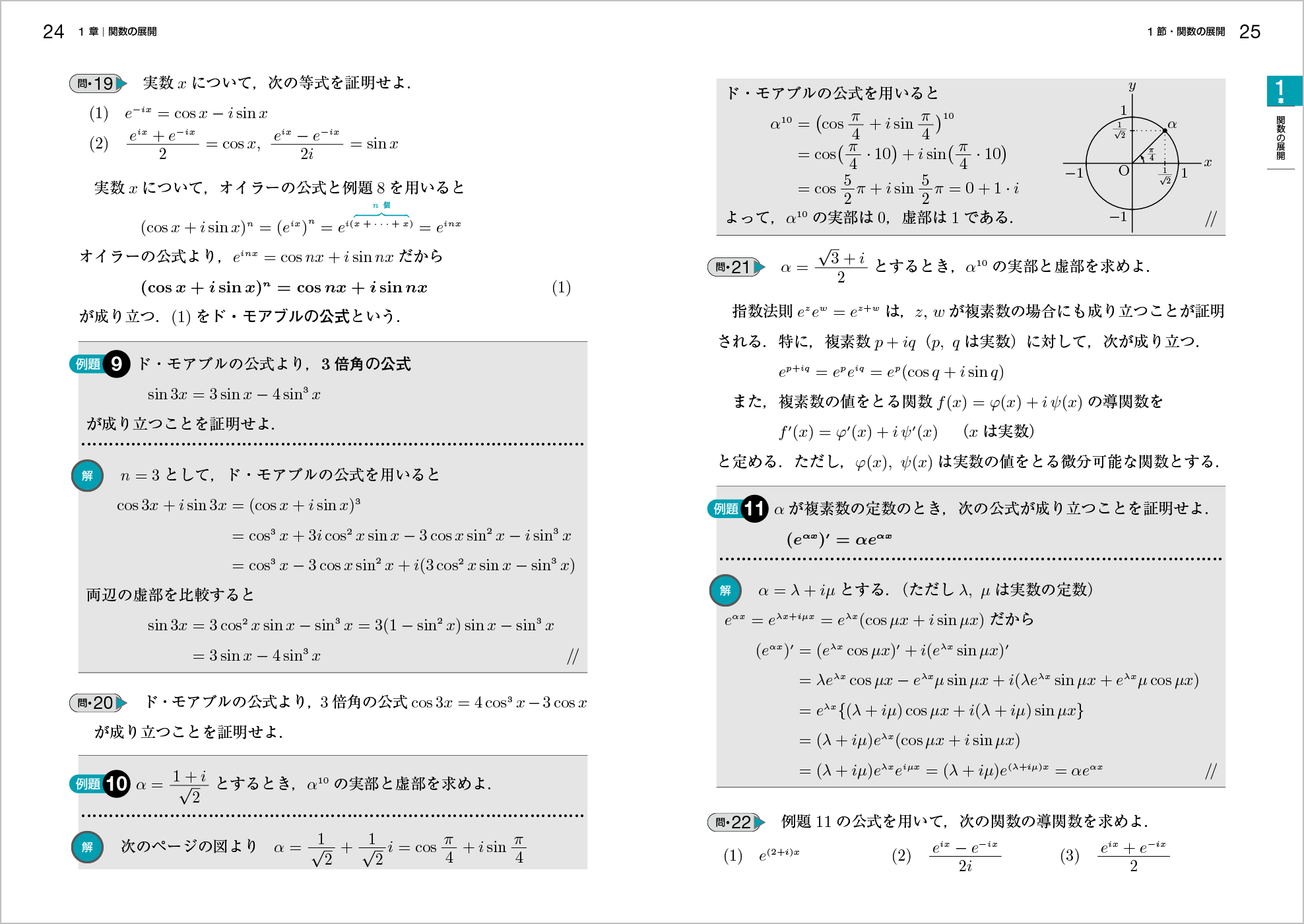
旧版の1・2「2重積分の計算」は内容が多いので,1・3を「積分の順序変更」,1・4を「立体の体積」として独立させました。
積分の順序を変更する時,積分領域から累次積分の積分範囲をとらえ直す必要があります。1・3「積分の順序変更」では,定着につながる例題を追加して,積分範囲の対応関係をとらえられるように図を工夫しました。3章 重積分
ポイント① 1・3「積分の順序変更」を独立させました。
ポイント② 積分の順序変更の定着につながる例題を追加しました。
ポイントをかくす
-
ページ紹介④極座標による2重積分の説明
-
極座標による2重積分では,最初に極座標による累次積分をイメージしやすくする簡単な例題を追加しました。2重積分を極座標変換によって求める時,極座標$(r,\ \theta)$の積分範囲がわかるように,直交座標の積分領域の図に工夫を加えています。
なお,旧版で扱っていた積分領域が異なる不等式で表されている場合の2重積分については補章p.151に移りました。3章 重積分
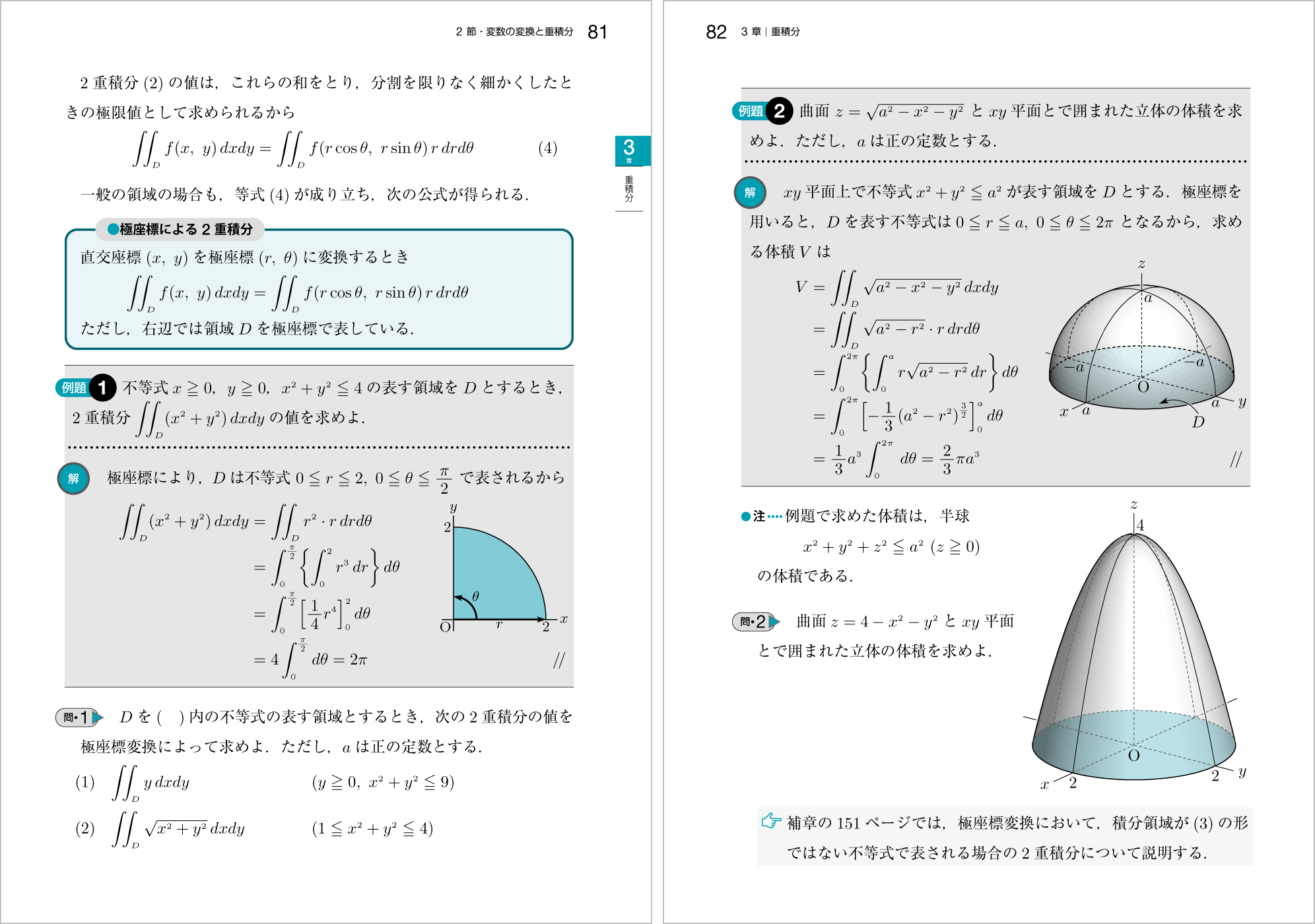
ポイント① 極座標による累次積分をイメージしやすくする簡単な例題を追加しました。
ポイント② 旧版の本文で扱っていた積分領域が異なる不等式で表される場合の2重積分については補章に移りました。
ポイントをかくす
補章 3章の補足

ポイント 旧版の本文で扱っていた内容です。授業の進度に合わせてご活用下さい。
ポイントをかくす
-
ページ紹介⑤微分方程式における独立変数 $t$ の導入
-
微分方程式は応用分野でよく扱われ,時間に伴う変化を調べることがよくあります。この章では,独立変数に$t$,従属変数に$x,\ y$を用いています。
また,全く同じ微分方程式でも,文字が変わると急に解けなくなることがあり,このことの原因として,ライプニッツの記法を使い慣れていないことが考えられます。実際,ライプニッツの記法$\Bigl(\frac{dx}{dt}\Bigr)$よりもラグランジュの記法$\Bigl(x'\Bigr)$の方が,書くときも楽なので,ついラグランジュの記法を使いがちです。しかしそれではライプニッツの記法はなかなか身につきません。応用分野でよく用いられるのもライプニッツの記法です。そうしたことを考慮して,この章に限りライプニッツの記法$\Bigl(\frac{dx}{dt}\Bigr)$を用いるようにして,ライプニッツの記法に慣れることができるようにしました。4章 微分方程式

ポイント 変数分離形の微分方程式の解法では,ライプニッツの記法は欠かせません。ライプニッツに記法に慣れることができるようにしました。
ポイントをかくす
-
ページ紹介⑥定数係数非斉次2階線形微分方程式の解法の見直し
-
従来は3つのパターンについてそれぞれ1つの解を求めさせて,最後に一般解を求めさせる構成となっていました。今回はこうした2段階の構成を見直して,まず未定係数法について説明し,2段階に分けずに最初から一般解を求めさせるように変更しました。
なお,旧版で扱っていた予想した解が斉次線形微分方程式の一般解と重なる場合については,補章のp.151に移りました。4章 微分方程式

ポイントをかくす
ポイント① 旧版では,1つの解を予想する時の解の形を表にまとめていましたが,新版では未定係数法による説明に変更しました。
ポイント② 新版では1つの解ではなく,一般解を求める例題に変更しました。
補章 4章の補足

ポイント① 旧版の本文で扱っていた予想した解が斉次線形微分方程式の一般解と重なる場合について補章に移りました。
ポイント② 旧版の本文で扱っていた内容です。授業の進度に合わせてご活用下さい。
ポイントをかくす
新 微分積分Ⅱ 問題集 改訂版
| 監修 | ||||
|---|---|---|---|---|
| 監修 | 高遠節夫(元東邦大学教授) |
|||
| 執筆 | ||||
| 執筆 | 久保康幸(弓削商船高等専門学校准教授) |
小谷泰介(釧路工業高等専門学校准教授) |
篠原知子(都立産業技術高等専門学校品川キャンパス教授) |
高橋正郎(久留米工業高等専門学校准教授) |
拜田稔(鹿児島工業高等専門学校教授) |
前田善文(長野工業高等専門学校名誉教授) |
松宮篤(明石工業高等専門学校教授) |
山下哲(木更津工業高等専門学校教授) |
|
| 校閲 | ||||
| 校閲 | 秋山聡(和歌山工業高等専門学校教授) |
大庭経示(米子工業高等専門学校教授) |
北見健(函館工業高等専門学校准教授) |
櫻井秀人(富山高等専門学校射水キャンパス准教授) |
佐藤一樹(一関工業高等専門学校講師) |
濵田俊彦(和歌山工業高等専門学校教授) |
山中聡(津山工業高等専門学校講師) |
横谷正明(津山工業高等専門学校教授) |
- 「新微分積分Ⅱ改訂版」に準拠した問題集です。
- B5判のゆったりとした紙面で学習していただけます。
- 充実した基本問題(Basic)や確認問題(Check)を解くことで,教科書の内容を確実に身につけていくことができます。
- 標準問題(Step up)や発展的な内容(Plus)も豊富にとりそろえていて,学生の学力に合わせて幅広くお使いいただけます。
- 基本問題(Basic)や確認問題(Check)を中心に数値を見直して刷新しました。
| 目次 | 1章 関数の展開関数の展開 |
|---|---|
2章 偏微分偏微分法/偏微分の応用 |
|
3章 重積分2重積分/変数の変換と重積分 |
|
4章 微分方程式1階微分方程式/2階微分方程式 |
-
ページ紹介①まとめ
-
教科書で学習した内容の要点をまとめています。
1章 関数の展開

-
ページ紹介②Basic(基本問題)
-
教科書の問の定着を確認する問題です。豊富な類題で基礎・基本を身につけます。
教科書の問に対応していて,できなかった場合は右側の教科書参照ページを見て,教科書で復習することができます。1章 関数の展開

ポイント 教科書に戻って復習できるよう,対応する教科書の問いを示しました。
ポイントをかくす
-
ページ紹介③Check(確認問題)
-
Basicの定着を確認する問題です。
Checkの解答ではBasicの問題を参照しているので,Checkでできなかった問題をBasicで復習することも可能です。。2章 偏微分
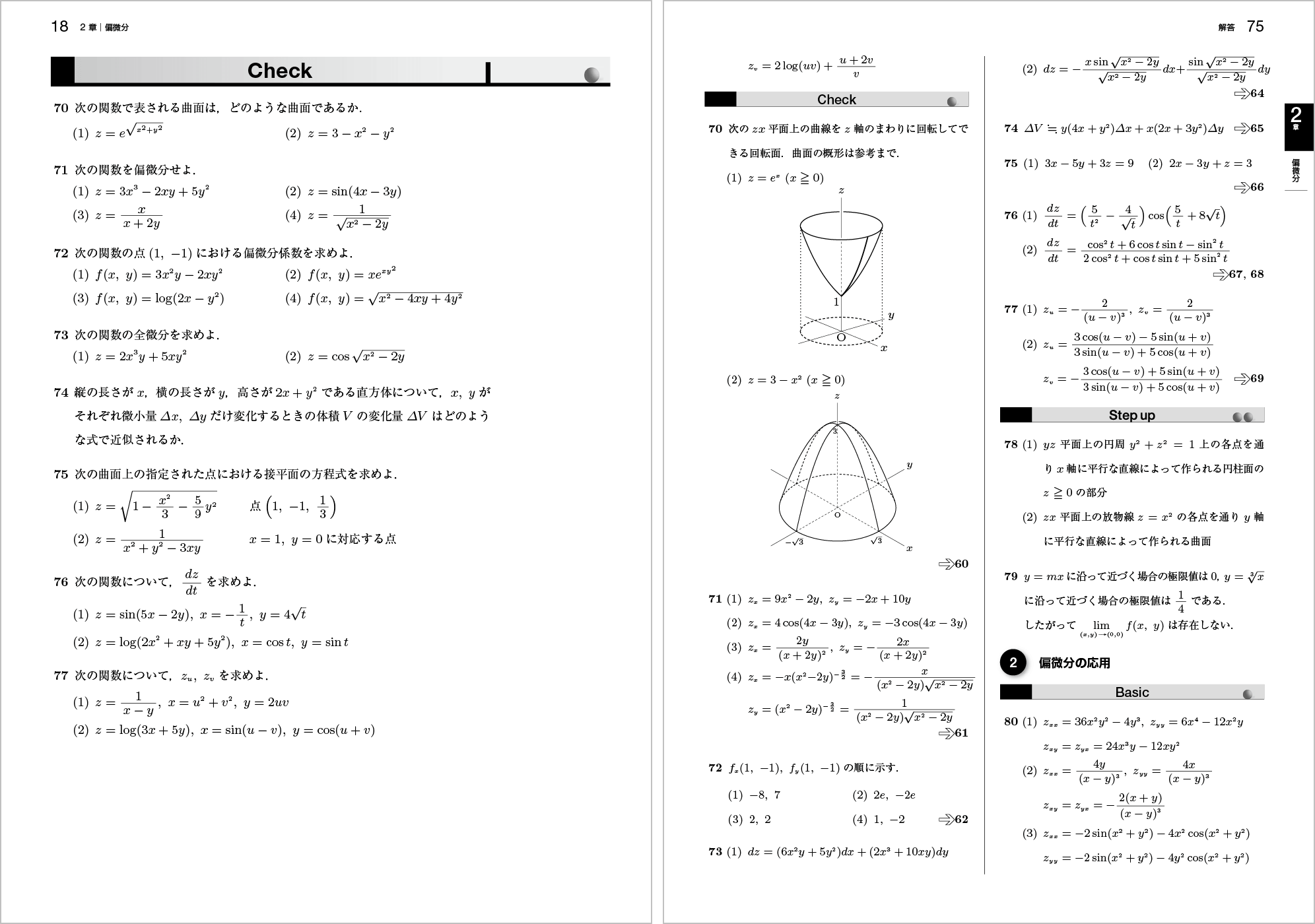
ポイント Basic(基本問題)に戻って復習できるよう,対応する問題番号を示しました。
ポイントをかくす
-
ページ紹介④Step up(標準問題)
-
基礎知識を応用させて解く問題です。例題の後には関連する問題が続くように構成して,より使いやすくなりました。
ここでは大学編入試験問題も取り上げています。3章 重積分

ポイント① 例題と問題がセットになっている使いやすい構成です。
ポイント② 大学編入試験問題を適宜取り上げています。
ポイントをかくす
-
ページ紹介⑤Plus(発展的内容と問題)
-
教科書では扱っていない発展的な内容を取り上げ,学生が自学自習で取り組むことができるようにしています。
ここでは大学編入試験問題も取り上げました。教科書の補章に関する問題も「補章関連」のところで取り上げるようにしています。3章 重積分

ポイント① 教科書では詳しく扱っていない「3重積分」の内容を例題も取り入れながら丁寧に扱っています。
ポイント② 教科書では詳しく扱っていない「3重積分の変数変換」の内容を例題も取り入れながら丁寧に扱っています。
ポイントをかくす

ポイント 教科書では詳しく扱っていない「ガンマ関数とベータ関数」の内容を例題も取り入れながら丁寧に扱っています。
ポイントをかくす
4章 微分方程式

ポイント 教科書では詳しく扱っていない「演算子法」の内容を例題も取り入れながら丁寧に扱っています。
ポイントをかくす

ポイント 教科書では詳しく扱っていない「完全微分方程式」の内容を例題も取り入れながら丁寧に扱っています。
ポイントをかくす
1章 関数の展開

ポイント Plusの最後には,補章に関する問題を集めた「補章関連」や,その他の補充問題を集めた「いろいろな問題」を設けています。
ポイントをかくす
-
ページ紹介⑥解答
-
Step upやPlusの解答には,詳しい解説をつけています。

新 微分積分Ⅱ

定価:1,870円(本体1,700円+税)
体裁:A5判・上製本 / 2色 / 188頁
ISBN:978-4-477-02685-5
定価:1,870円(本体1,700円+税)
体裁:A5判・上製本 / 2色 / 188頁
ISBN:978-4-477-02685-5
| 著者 | |||||||
|---|---|---|---|---|---|---|---|
| 著者 | 齋藤純一(都立産業技術高等専門学校准教授) |
高遠節夫(東邦大学理学部訪問教授) |
野澤武司(長岡工業高等専門学校教授) |
||||
濵口直樹(長野工業高等専門学校教授) |
前田善文(長野工業高等専門学校名誉教授) |
山下哲(木更津工業高等専門学校教授) |
|||||
| 校閲 | |||||||
| 校閲 | 有本茂(津山工業高等専門学校教授) |
岡田章三(岐阜工業高等専門学校教授) |
岡中正三(呉工業高等専門学校名誉教授) |
金子真隆(東邦大学薬学部教授) |
蔵岡誉司(米子工業高等専門学校教授) |
佐藤達郎(大分工業高等専門学校教授) |
佐藤敏行(元仙台高等専門学校教授) |
高橋正郎(久留米工業高等専門学校准教授) |
徳能康(仙台高等専門学校教授) |
西垣誠一(沼津工業高等専門学校教授) |
藤島勝弘(苫小牧工業高等専門学校教授) |
松尾幸二(一関工業高等専門学校教授) |
松宮篤(明石工業高等専門学校教授) |
「新 微分積分Ⅱ」のねらい
「新微分積分Ⅱ」では,「新微分積分Ⅰ」で学習した1変数関数の微分法と積分法に続き,2変数関数の微分法と積分法,さらに関数の級数展開や微分方程式の基礎を学習します。
本書では「新微分積分Ⅰ」とのつながりを大切にしながら,より深い内容を早めに使いこなせるようになることを目指しました。
| 目次 | 1章 関数の展開関数の展開 |
|---|---|
2章 偏微分偏微分法/偏微分の応用 |
|
3章 重積分2重積分/変数の変換と重積分 |
|
4章 微分方程式1階微分方程式/2階微分方程式 |
|
1章詳説 関数の展開詳説関数の展開 |
-
空間図形を見やすく
-
新微分積分Ⅰでは1変数の微分や積分を学習しますが,新微分積分Ⅱでは2変数の微分(偏微分)や積分(重積分)を学習します。
2変数を扱う場合はしっかりとした空間的なイメージが必要になります。新微分積分Ⅱでは見やすい空間図形の図を多く取り入れました。2章 偏微分
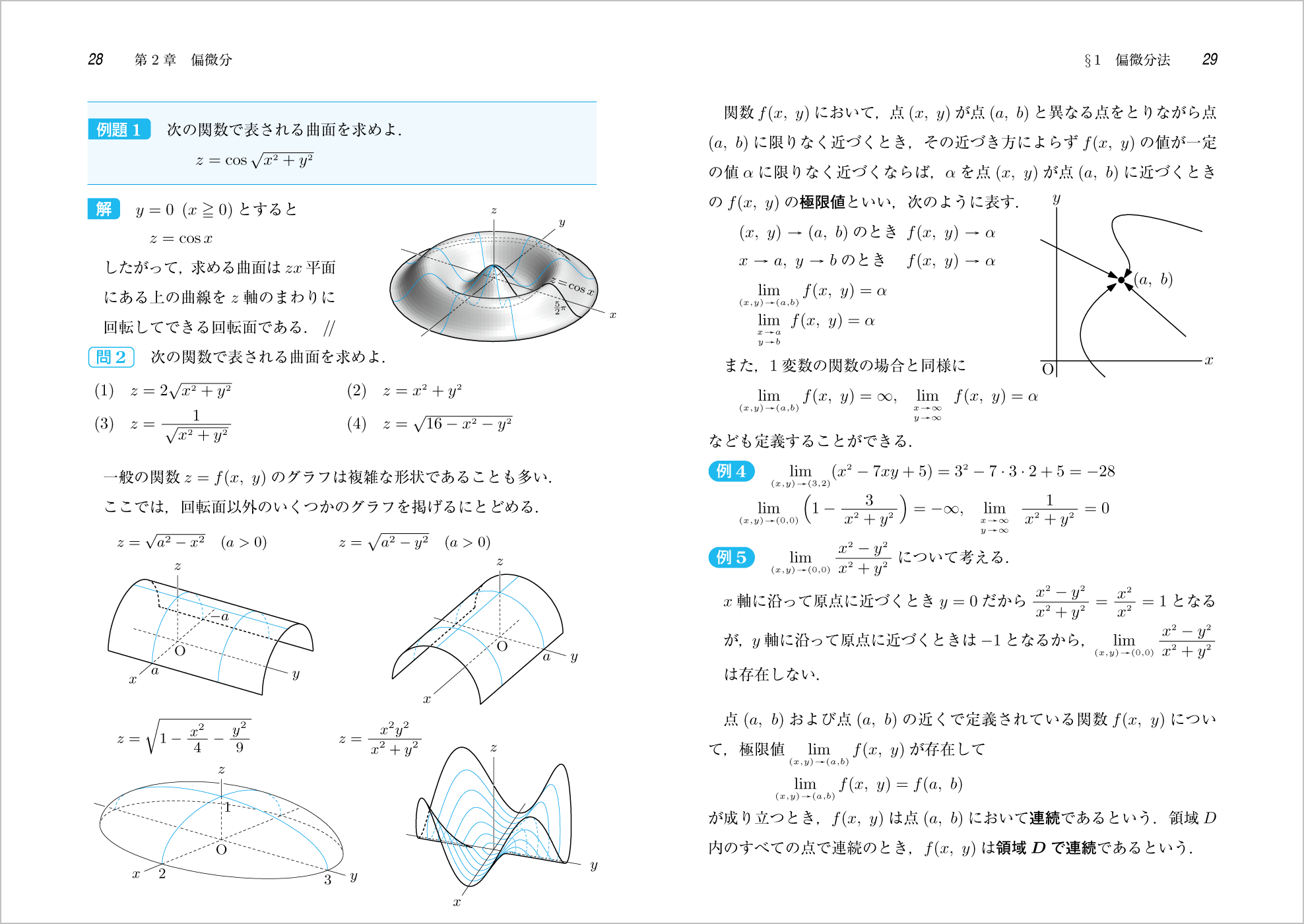

ポイント 回転面や回転面以外の曲面の特徴をとらえさせる場面では,その補助となる図を添えました。
ポイントをかくす
3章 重積分
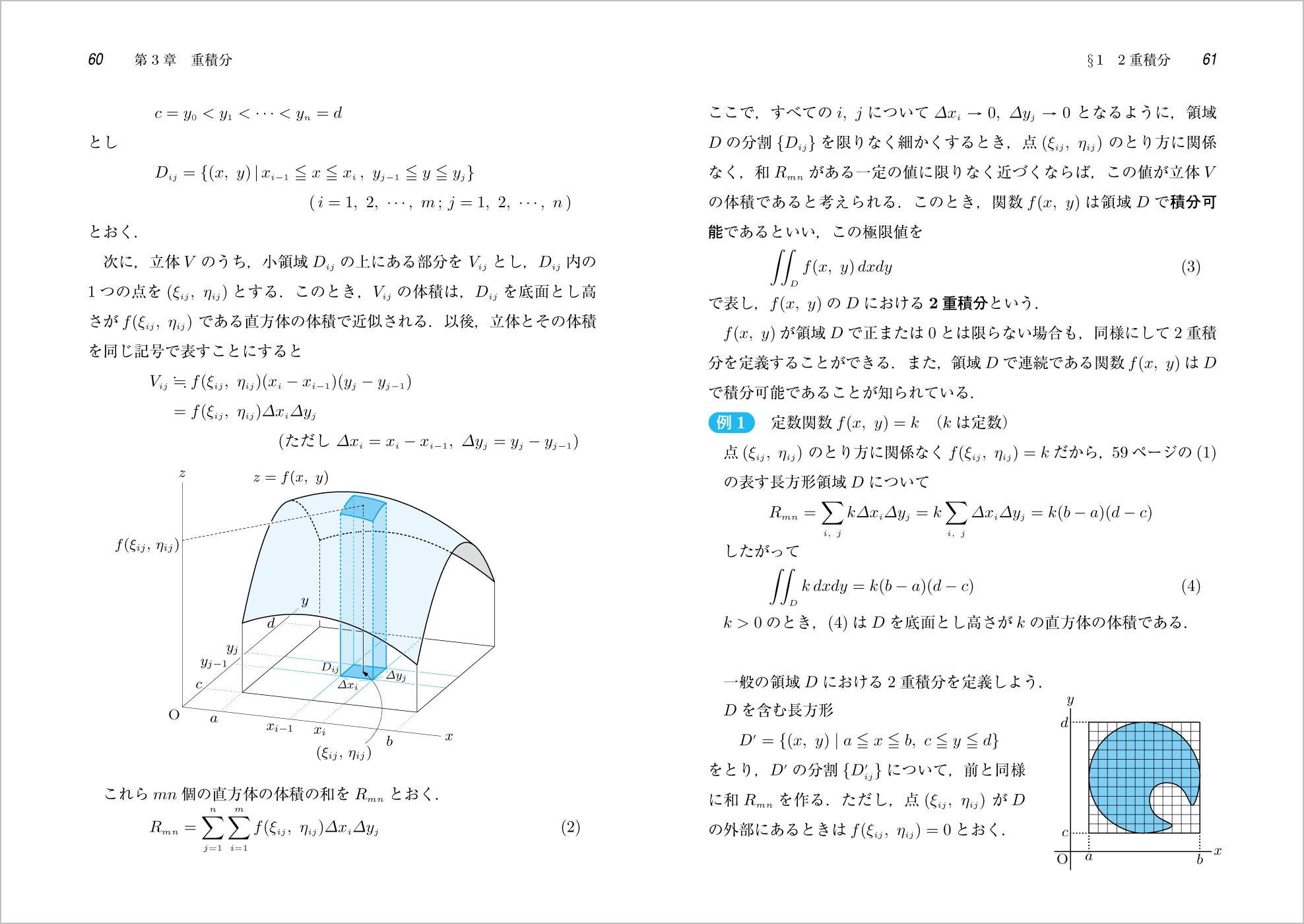

ポイント 2重積分の定義を視覚的にとらえさせる図です。
ポイントをかくす


ポイント 2重積分によって立体の体積を求める際には,領域と立体をきちんととらえることが大切です。
計算問題では,その手助けとなる図を豊富に取り入れています。
ポイントをかくす
-
全微分の導入の工夫
-
従来は接平面の説明にページを割いて,そこから全微分の定義につなげていましたが,新微分積分Ⅱでは,図を活用しながら全微分の意味を考えさせていく構成にしました。接平面の定義は最後に取り扱います。
2章 偏微分


ポイント 全微分の導入では,まず1次関数の場合での $z$ の変化量をとらえ,一般の関数の場合につなげていきます。
ポイントをかくす
-
微分方程式における独立変数の導入
-
微分方程式は応用分野でよく扱われ,特に時間に伴う変化を調べることがよくあります。そこでこの章では,独立変数に $t$,従属変数に $x$,$y$ を用いることにしました。
また,全く同じ微分方程式でも,文字が変わると急に解けなくなるという話を聞きます。このことの原因として,ライプニッツの記法 $\displaystyle \left( \frac{dx}{dt} \right)$ を使い慣れていないことが考えられます。実際,ライプニッツの記法 $\displaystyle \left( \frac{dx}{dt} \right)$ よりもラグランジュの記法 $\left( x' \right)$ の方が,書くときも楽なので,ついラグランジュの記法を使いがちです。しかしそれではライプニッツの記法はなかなか身につきません。また,応用分野でよく用いられるのはライプニッツの記法です。そうしたことを考慮して,この章に限りライプニッツの記法 $\displaystyle \left( \frac{dx}{dt}, \frac{d^2x}{dt^2} \right)$ を用いるようにして,ライプニッツの記法に慣れていただく機会を設けました。4章 微分方程式
ポイント 変数分離形の微分方程式の解法では,ライプニッツの記法は欠かせません。ライプニッツの記法に慣れていただけるようにしました。

-
1章詳説「関数の展開」を設置
-
従来は補章「(続)関数の展開」として1章「関数の展開」を補足する位置付けでしたが,今回は1章を学ぶ代わりに,この章だけで学ぶことができるように章として独立させました。1章では最低限必要な事項を身に付けることができますが,1章詳説では1章よりさらに詳しく学習することができます。
1章詳説 関数の展開
ポイント 従来の補章「(続)関数の展開」の内容を1章「関数の展開」に組み込んで構成しました。

ポイント 級数についてもう少し詳しく教えたい場合にご活用いただけます。テイラーの定理やテイラー展開などについても扱っています。

-
巻末の重要事項のまとめ
-
本書に関連する重要事項を巻末にまとめました。2年以降の教科書の巻末に設けています。関連ある内容を一箇所にまとめることで,全体像が把握しやすくなりました。参照ページがあるので振り返りも可能です。学生の自習の際にもお使いいただけます。
付録
ポイント 新基礎数学や新微分積分Ⅰで学習したものの中で,よく使うものを取り上げました。


ポイント 微分方程式の解法を整理したものです。微分方程式の解法について確認したり復習したりする時に便利です。
ポイントをかくす


ポイント 微分方程式の解法を整理したものです。微分方程式の解法について確認したり復習したりする時に便利です。
ポイントをかくす
新 微分積分Ⅱ 問題集

定価:990円(本体900円+税)
体裁:B5判 / 112頁
ISBN:978-4-477-02687-9
定価:990円(本体900円+税)
体裁:B5判 / 112頁
ISBN:978-4-477-02687-9
| 著者 | |||
|---|---|---|---|
| 著者 | 阿部弘樹(東京経済大学全学共通教育センター) |
新井一道(小山工業高等専門学校名誉教授) |
高遠節夫(東邦大学理学部訪問教授) |
西浦孝治(福島工業高等専門学校教授) |
野澤武司(長岡工業高等専門学校教授) |
濵口直樹(長野工業高等専門学校教授) |
|
| 校閲 | |||
| 校閲 | 嶋野和史(文教大学教育学部講師) |
高橋正郎(久留米工業高等専門学校准教授) |
|
谷垣美保(仙台高等専門学校准教授) |
菱川洋介(岐阜大学教育学部助教) |
「新 微分積分Ⅱ 問題集のねらい
「新微分積分Ⅱ」に準拠した問題集です。
学習内容の確実な定着を図る基本問題・確認問題,応用力をつける標準問題,課題研究「PLUS」の構成で,学力に合わせて幅広くお使いいただけます。
| 目次 | 1章 関数の展開関数の展開/PLUS |
|---|---|
2章 偏微分偏微分法/偏微分の応用/PLUS |
|
3章 重積分2重積分/変数の変換と重積分/PLUS |
|
4章 微分方程式1階微分方程式/2階微分方程式/PLUS |
|
1章詳説 関数の展開詳説関数の展開/PLUS |
-
ゆったりとしたB5判サイズ
-
これまでの問題集はA5判でしたが,新シリーズではゆったりとしたB5判にしました。
ゆったりとした紙面に豊富な類題を取りそろえ,余白には教科書の参照ページを設けたりしています。1章 関数の展開


ポイント ゆったりとした紙面にたくさんの類題を取りそろえ,BASIC(基本問題)の余白には教科書の参照ページを設けました。
ポイントをかくす
-
BASIC(基本問題)の充実
-
「BASIC」は基礎知識を身につけさせる問題です。
従来の基本問題には,もっと多くの問題を載せて欲しいという要望をいただいておりましたので,新シリーズのBASICでは,教科書の問と対応させた類題を取りそろえることで,基礎・基本の定着が図れるようにしました。
教科書の参照ページをわかりやすく示したので,対応する教科書の問に振り返るのも容易です。4章 微分方程式

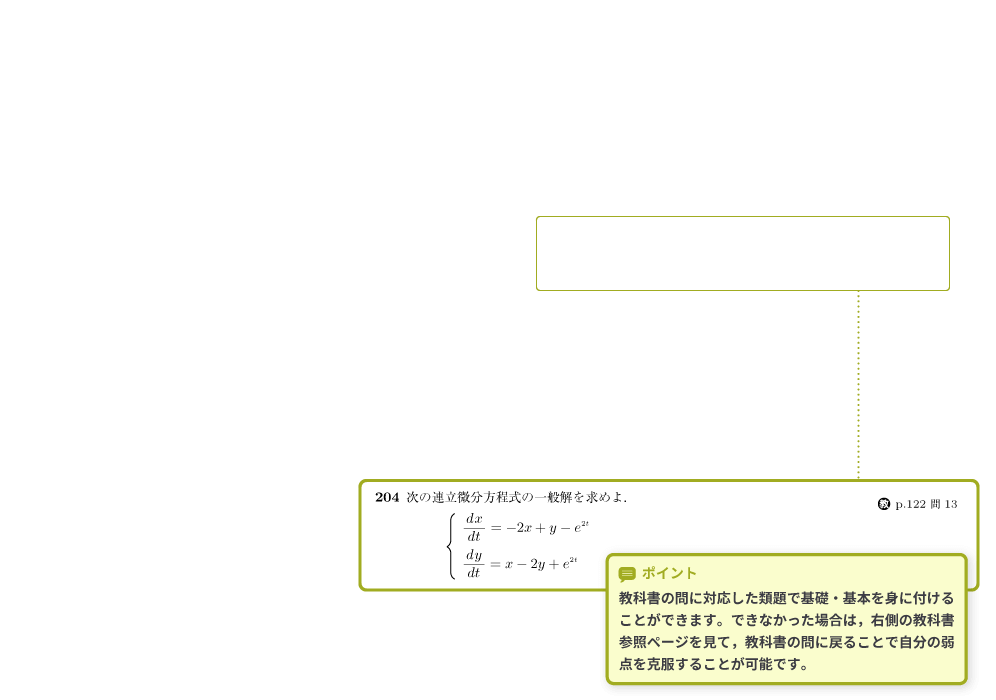
ポイント 教科書の問に対応した類題で基礎・基本を身に付けることができます。できなかった場合は,右側の教科書参照ページを見て,教科書の問に戻ることで自分の弱点を克服することが可能です。
ポイントをかくす
-
CHECK(確認問題)の新設
-
「CHECK」はBASIC(基本問題)の定着を確認する問題です。
BASICの問題の中で典型的なものを1ページにまとめています。BASICに自信のある方は,最初にCHECKからお使いいただくことも可能です。
CHECKの解答には,関連するBASICの問題番号を示しているので,できなかった問題があれば,BASICに戻って復習するのも容易です。4章 微分方程式

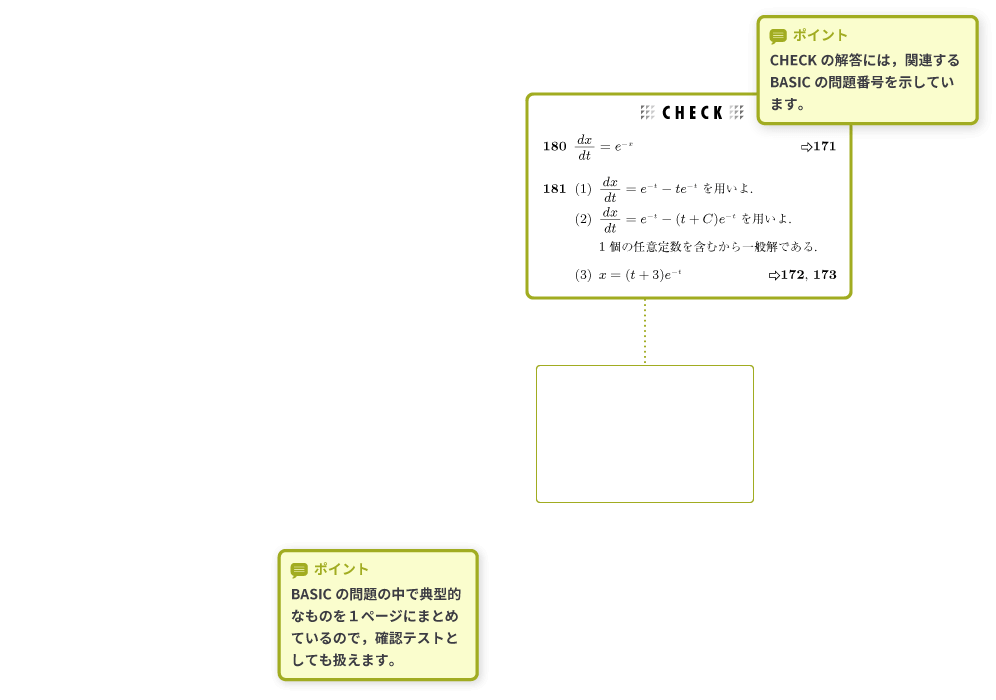
ポイント① BASICの問題の中で典型的なものを1ページにまとめているので,確認テストとしても扱えます。
ポイント② CHECKの解答には,関連するBASICの問題番号を示しています。
ポイントをかくす
-
応用力を育てるSTEP UP(標準問題)
-
「STEP UP」は,これまで学習してきた基礎知識を応用させて解く問題です。
考え方や解き方を示したほうがよいところでは,「例題」として考え方や解き方を示し,直後に例題に関連する問題を取り入れました。
ここでは大学編入試験問題も取り上げています。2章 偏微分

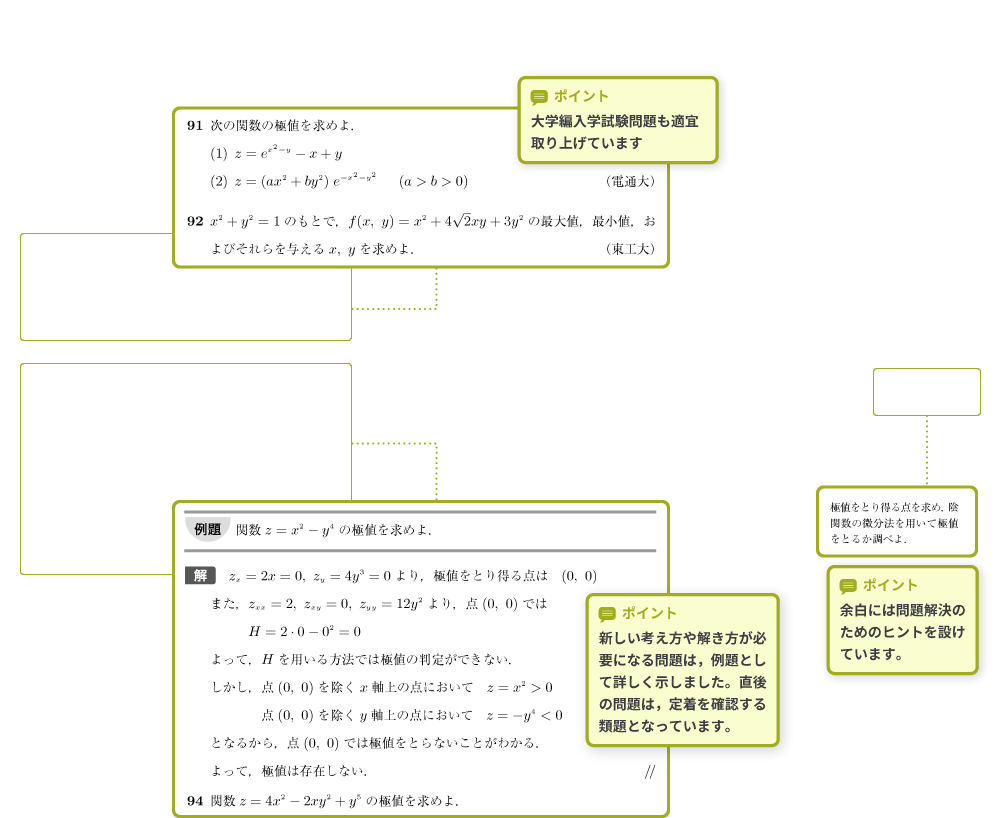
ポイント① 大学編入学試験問題も適宜取り上げています。
ポイント② 新しい考え方や解き方が必要になる問題は,例題として詳しく示しました。直後の問題は,定着を確認する類題となっています。
ポイント③ 余白には問題解決のためのヒントを設けています。
ポイントをかくす
-
発展的な内容のPLUS(課題研究)
-
「PLUS」では,教科書で以前扱っていた内容や,教科書で詳しく扱っていない発展的な内容を取り上げ,学生が自分自身で考えることができるように本文や解答を工夫しています。
ここでは大学編入試験問題も取り上げています。3章 重積分

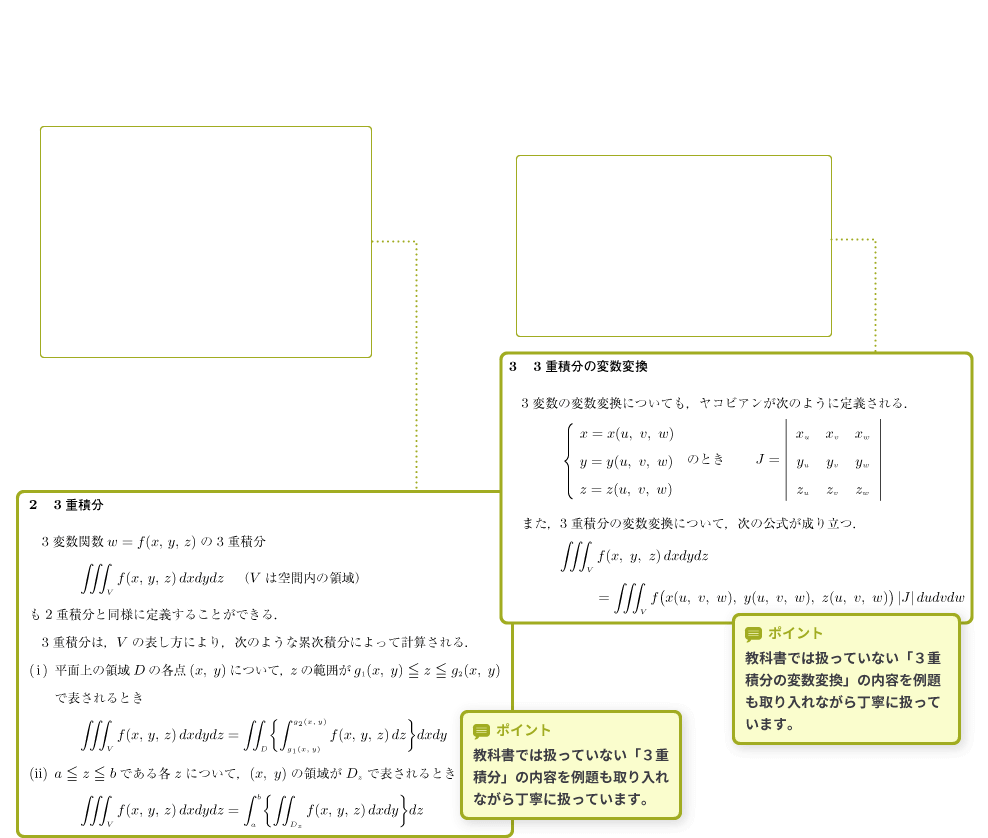
ポイント① 教科書では扱っていない「3重積分」の内容を例題も取り入れながら丁寧に扱っています。
ポイント② 教科書では扱っていない「3重積分の変数変換」の内容を例題も取り入れながら丁寧に扱っています。
ポイントをかくす


ポイント 教科書では扱っていない「ベータ関数とガンマ関数」も例題も取り入れながら丁寧に扱っています。
ポイントをかくす
4章 微分方程式


ポイント 教科書では扱っていない「演算子法」の内容も例題も取り入れながら丁寧に扱っています。
ポイントをかくす


ポイント 教科書では扱っていない「完全微分方程式」の内容も例題を取り入れながら丁寧に扱っています。
ポイントをかくす
2章 偏微分

ポイント PLUSでは,発展問題として大学編入試験問題を取り上げているところもあります。
ポイントをかくす
教科書新数学シリーズ
教材・資料











































