パスカル｜単位プラス

Processing math: 47%

定義：

$1\,$ $\text{m}^2$ の面積あたり $1\,$ $\text{N}$ の力が作用するときの圧力

SI基本単位による表記：

$\text{kg/m} \cdot \text{s}^2$

ブレーズ・パスカル: 圧力の単位パスカルは，フランスの科学者ブレーズ・パスカル（1623年〜1662年）の名前からつけられました。

[Public domain]
パスカルは，物理学，数学などさまざまな分野で知られる科学者です。中でも「人間は考える葦（あし）である」という名言を残した哲学者として知られています。

葦は，現在ではヨシと呼ばれる川や湖などの水際に見られるイネ科の多年草です。人間は自然の中で最も弱い存在だが，思考する存在であるところに偉大さがある，ということを示した言葉です。

葦は，現在ではヨシと呼ばれる川や湖などの水際に見られるイネ科の多年草です。人間は自然の中で最も弱い存在だが，思考する存在であるところに偉大さがある，ということを示した言葉です。

[Public domain]

パスカルの原理: 哲学者として有名なパスカルですが，物理学でも重要な発見をしています。「閉じ込められた液体の中では，圧力はあらゆる方向に同じ大きさで伝わる」というパスカルの原理です。

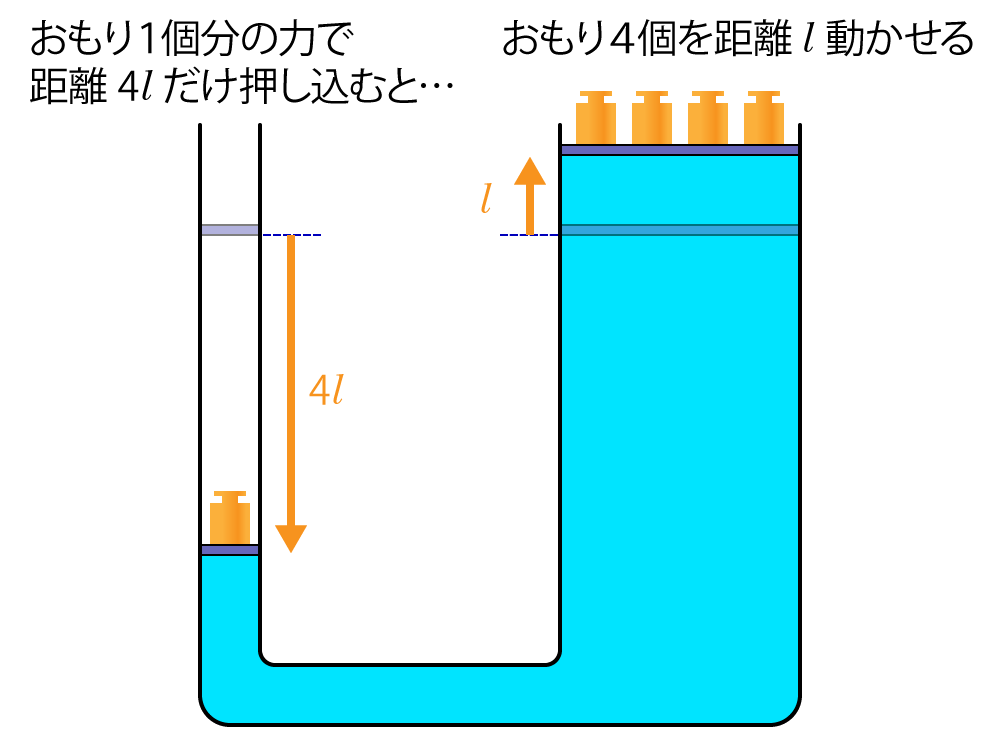
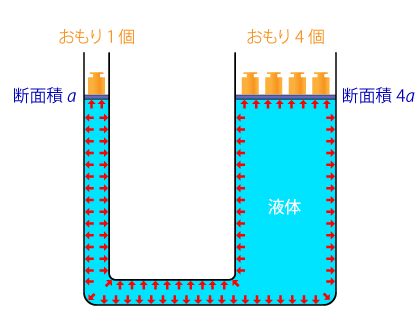
例えば，図のような口の断面積の異なる管に液体を満たした場合，面積が $a$ の管側にのせた１個のおもりは，面積が $4a$ の管側にのせた４個のおもりとつり合います。

この原理を利用すると，小さな力で質量の大きい物体を動かすことができるので，自動車の油圧ブレーキや油圧ジャッキなど身の回りのさまざまなものに応用されています。（→図をクリック）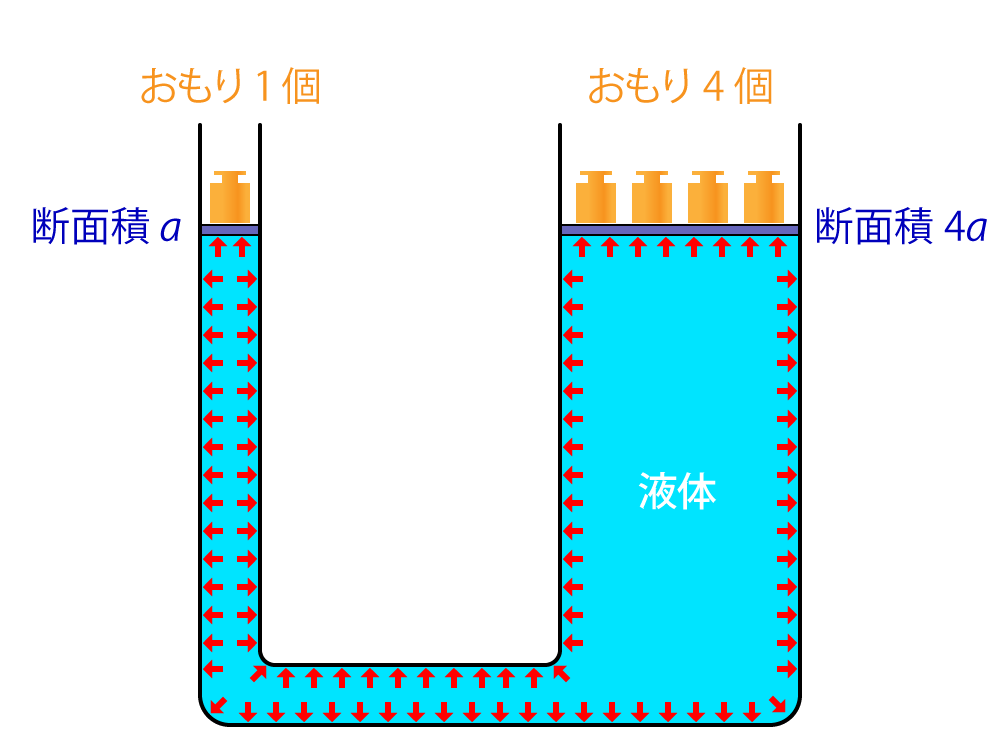

$1\text{ Pa}$ ってどのくらい？

単１マンガン乾電池にはたらく重力がおよそ

$1\text{ N}$ です。これが，

$1\text{ m}^2$ の面に乗っているときにその面から受ける圧力が

$1\text{ Pa}$ なのですが，

$1\text{ m}^2$ というと学校の机 4 個分という広い面です。これではちょっと実感しづらいですね。

もう少し小さな面を考えてみましょう。
一円玉を手のひらに置くことを考えます。

一円硬貨 [Public domain]

一円硬貨は質量

$1.0\text{ g}$ ，直径

$20\text{ mm}$ です。重力加速度

$g = 9.8$

$\text{ m/s}^2$ より，手のひらにはたらく圧力

$P$ は，次のように求められます。

$\begin{align} P &= \frac{F}{S} = \frac{mg}{S}\\ &= \frac{1.0 \times 10^{-3} \,\text{kg} \times 9.8 \,\text{m/s}^2 }{(10 \times 10^{-3} \,\text{m} )^2 \times \pi}\\ &\fallingdotseq 31 \,\text{Pa}\\ \end{align}$

……意外と大きいですね。

[Public domain]

一円玉よりも軽いものというと……紙ならどうでしょう。
紙の厚さは坪量（つぼりょう）で表します。坪量の単位は

$\text{ g/m}^2$ ，つまり，

$1\text{ m}^2$ あたりの紙の質量です。これは，圧力の計算に大変都合がいいですね。

さて， $1\text{ Pa}$ に近い紙というと『ペラペラではなく，しっかりめのチラシ』に使われる用紙の坪量が $104.7\text{ g/m}^2$ です。
この紙を $1\text{ cm}$ 角に切って手のひらに置くことを考えると，圧力 $P$ は次のように求められます。

紙の種類	坪量〔 $\text{ g/m}^2$ 〕
新聞紙（超軽量紙）	$43$
一般的なコピー用紙	$64$
官製はがき	$209$
工作用紙	$350$

　
さて，

$1\text{ Pa}$ に近い紙というと『ペラペラではなく，しっかりめのチラシ』に使われる用紙の坪量が

$104.7\text{ g/m}^2$ です。
この紙を

$1\text{ cm}$ 角に切って手のひらに置くことを考えると，圧力

$P$ は次のように求められます。

$\begin{align} P &= \frac{F}{S} = \frac{mg}{S}\\ &= \frac{ 104.7 \times 10^{-3} \,\text{kg/m}^2 \times ( 1 \times 10^{-2} \,\text{m})^2 \times 9.8 \,\text{m/s}^2 }{ ( 1 \times 10^{-2} \,\text{m})^2 }\\ &\fallingdotseq 1.03 \,\text{Pa}\\ \end{align}$

標準大気圧: 地球は大気に覆われているので，地表にいるわたしたちには，その大気による圧力がはたらいています。その大きさはおよそ $100000\text{ Pa}$ です。
大気圧は標高などによって変わるので，平均海水面における平均気圧から標準大気圧が定められており，その大きさは $101325\text{ Pa}（= 1013.25\text{ hPa}）$ です。