定義：
$1\,$$\text{s}$ 間に $1\,$$\text{m/s}$ の加速度
-
$1\text{ m/s}^2$ ってどのくらい？
-
通勤用電車の加速度が，およそ $0.6$ ~ $1.0\text{ m/s}^2$ です。$1\text{ m/s}^2$に近いものとしては，京急電鉄の新1000形車両（加速度 $0.97\text{ m/s}^2$）が挙げられます。
-
$100\text{ m}$ 競争にみる加速度
-
加速度とは，単位時間あたりの速度の変化率のことです。
ジャマイカのウサイン・ボルト選手が，世界陸上競技選手権（2009年・ベルリン）で男子 $100\,\text{m}$ の世界記録を出したときのラップタイムから，加速度を求めてみましょう。
ボルト選手のラップタイムは左表の通りです。これをグラフにすると右の図のようになります。距離〔$\text{m}$〕 タイム〔$\text{s}$〕 $0$ $0$ $20$ $2.89$ $40$ $4.64$ $60$ $6.31$ $80$ $7.92$ $100$ $9.58$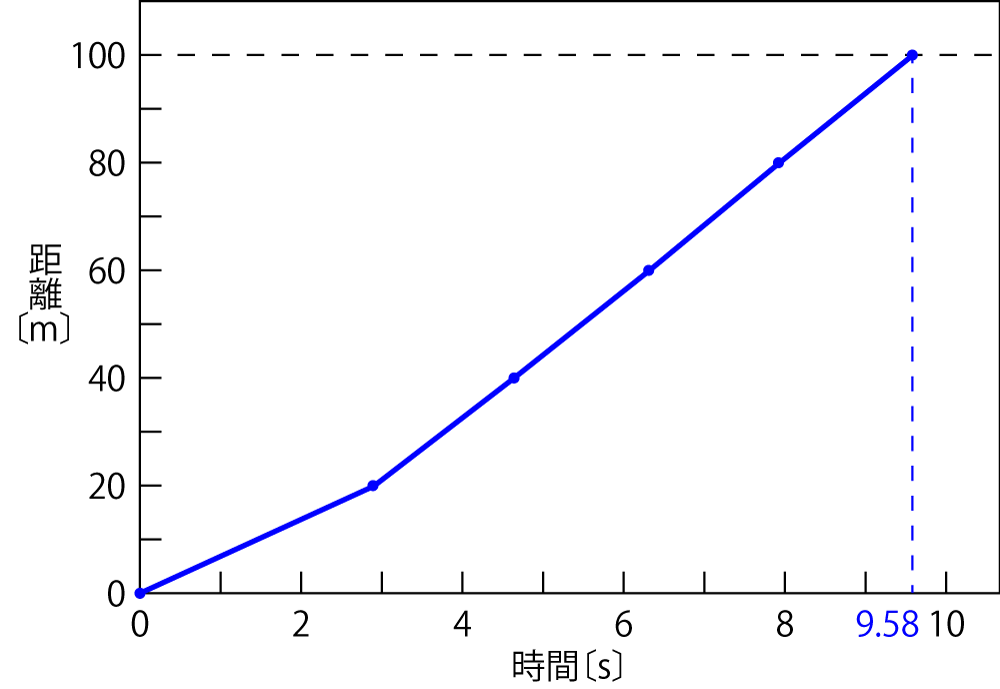 
最初の $20\text{ m}$ までにやや時間がかかっているものの，後はほぼ一定のグラフに見えます。
では，各区間の平均の速さを求めて見ましょう。
例えば，$20$ ~ $40\text{ m}$ の区間の速さ $v$ は，距離 $l$，時間 $t$ から次のように求められます。\begin{align} v &= l \div t\\ &= ( 40 - 20 )\,\text{m} \quad/\quad ( 4.64 - 2.89 )\,\text{s}\\ &= 11.43\,\text{m/s} \end{align}
同様に全区間の速さを求めます。平均の速さなので，各区間の中央の時間でプロットすると右のグラフのようになります。区間〔$\text{m}$〕 区間の中央の時間〔$\text{s}$〕 平均の速さ〔$\text{m/s}$〕 $0 - 20$ $1.445$ $6.92$ $20 - 40$ $3.765$ $11.43$ $40 - 60$ $5.475$ $11.98$ $60 - 80$ $7.115$ $12.42$ $80 - 100$ $8.750$ $12.05$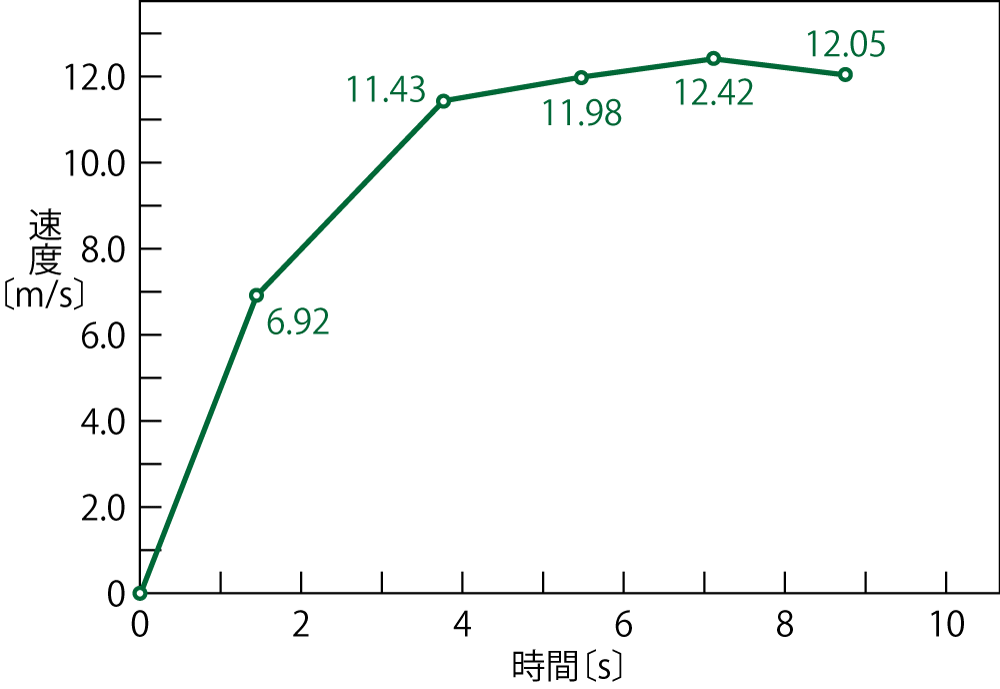 
ずっと一定の速さで走っていたのではなく，最初の２区間で傾きが急で，後はほぼ一定であることがわかります。
この傾きが加速度です。
最初の区間の加速度 $a_{1}$，次の区間の加速度 $a_{2}$ は，それぞれ次のように求められます。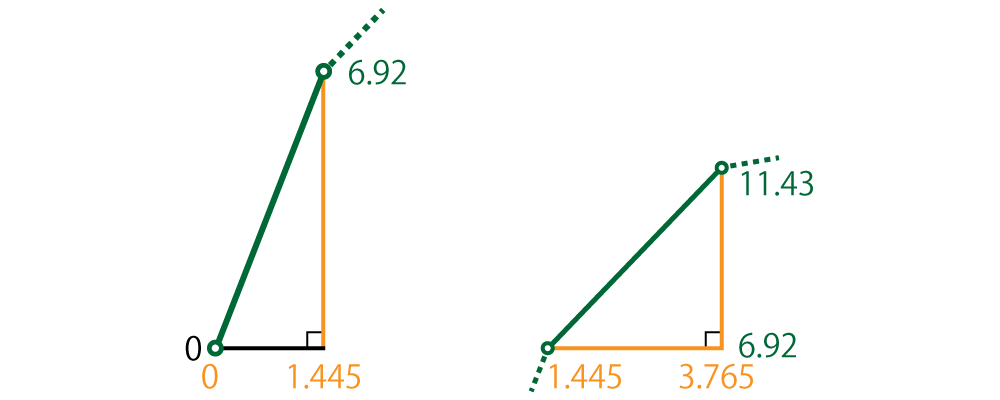
\begin{align} a_{1} &= v \div t\\ &= ( 6.92 - 0 )\,\text{m/s} \quad/\quad ( 1.445 - 0 )\,\text{s}\\ &= 4.79\,\text{m/s}^2\\ a_{2} &= v \div t\\ &= ( 11.43 - 6.92 )\,\text{m/s} \quad/\quad ( 3.765 - 1.445 )\,\text{s}\\ &= 1.92\,\text{m/s}^2\\ \end{align}
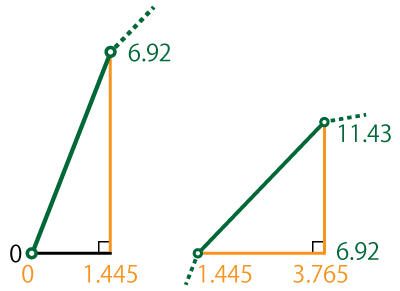同様に計算すると $a_{3} = 0.32\text{ m/s}^2$ となります。瞬発力で一気に最高速に到達し，残りはその速さを維持しているとわかります。
-
重力加速度
-
静止していた物体が真下に落下する運動を自由落下運動といいます。自由落下運動では，物体は一定の割合で速くなっていきます。このときの加速度を重力加速度 $g$ といい，地表付近では $9.8\text{ m/s}^2$ です。
重力加速度は地球の地点によって変化するので，標準重力加速度 $g_{0} = 9.80665\text{ m/s}^2$ が定められています。
