小学校算数科の編集担当になった当初の教科書（昭和49年度版「新算数」）を見ていたら、小さい挿絵ではありますが懐かしい場面がありました。

ページ中段に、やかんとなべのイラストがあります。やかんは、１デシリットルますで５はい。なべは、１デシリットルますで10はい。と書いてありますが、イラストのやかんとなべの容積の比は、本当に１：２になっているでしょうか？

共に大凡（おおよそ）高さの等しい円柱とみて計算してみましょう。高さが等しいのですから容積の比は底面積の比になります。底面積の比は紙面に表れている長さの比の2乗になりますから、なべの直径（半径）がやかんのそれの $\sqrt{2}$ 倍になっていればよいわけです。

紙面上のイラストを実際に測ってみると、図のような寸法になっていました。

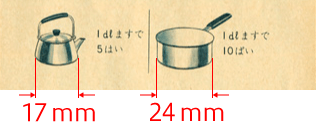
やかんは 17 mm、なべは 24 mm です。24 $\div$ 17 $\fallingdotseq$ 1.41 となり、$\sqrt{2}$ に極めて近い数値になりました。

2005.12.01