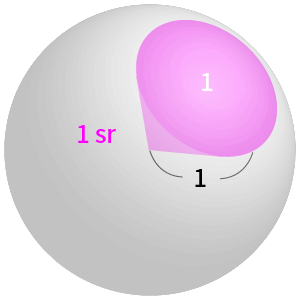
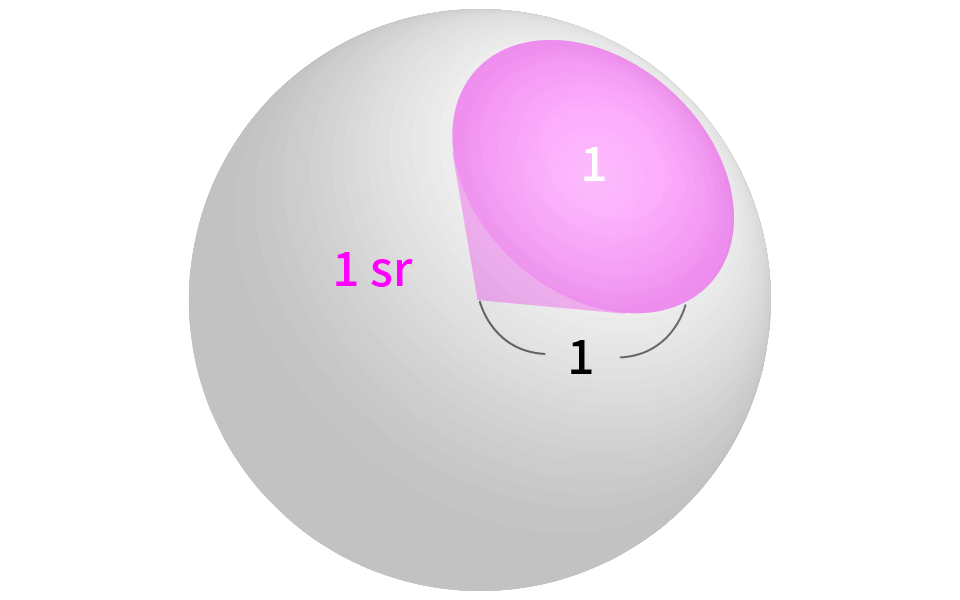
定義:
半径1の球において、球面を面積1で切り取る立体角
-
ラジアンとステラジアン
-
立体角というのは、錐体の頂点からその錐体の側面によって区切られた部分の広がり度合いを表した量です。
視野に占める割合のようなものと考えるといいでしょう。例えば、バスケットボールを目から 10 cm ほどのところに掲げれば、視野のほとんどがバスケットボールに覆われます。立体角が大きい状態です。そして、腕を伸ばして掲げれば、バスケットボールは視野のわずかしか遮りません。立体角の小さい状態です。
こうした量を測定する単位が、sr(ステラジアン)です。steradian というのは、立体を意味する stereo と、角度の単位 radian からできた言葉です。
rad(ラジアン)は、平面上の角度を単位円(半径1の円)における弧の長さで定義した単位でした。この概念を空間に拡張し、立体角を単位球(半径1の球)における球面の面積で定義したのが、sr です。
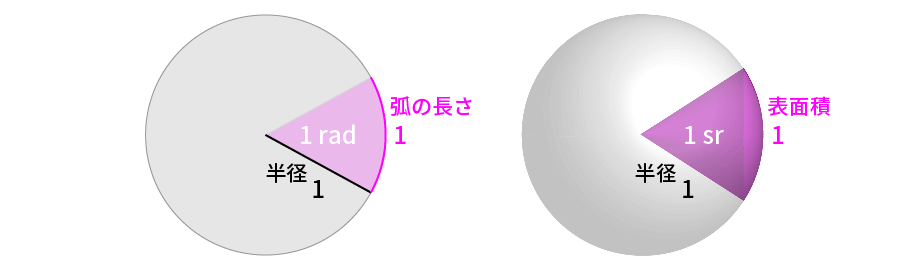

単位球の表面積は $4 \pi$ なので、$\dfrac{1}{4 \pi} = 0.0795774…$ より、1 sr は球面のおよそ8%を覆う大きさとわかります。
-
頂角と立体角の関係
-
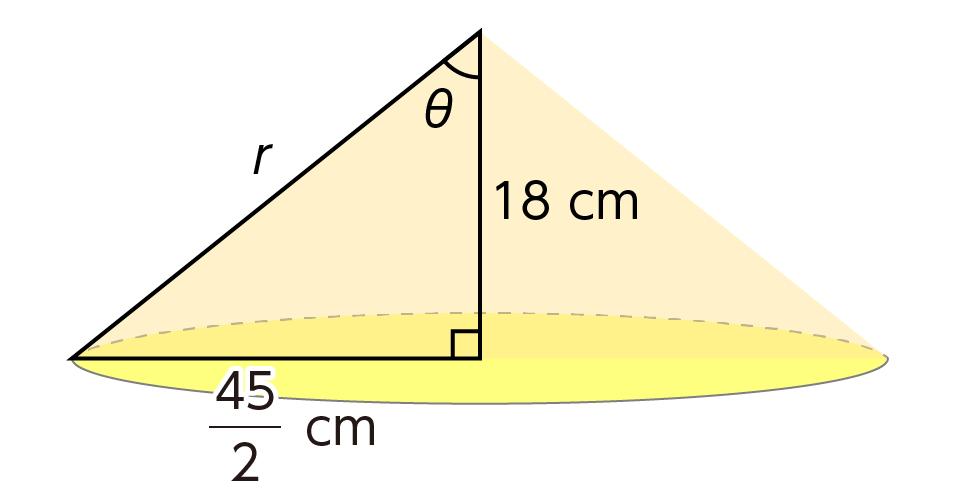
ステラジアンの大きさの見当をつけるため、円錐状の立体を真横から見たときの頂角の半分を $\theta$ とし、対応する立体角 $\omega$ がいくつになるか計算してみましょう。
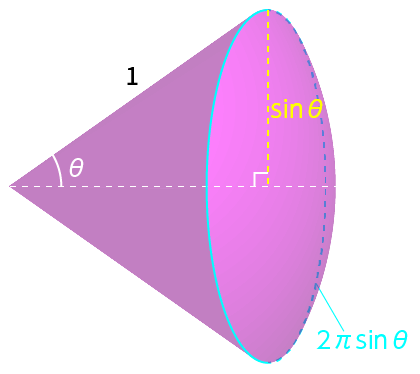
この立体が球を切り取る円(図の水色部分)を考えると、その半径は $\sin \theta$ ですから、この円周は $2 \pi \sin \theta$ となります。
これを角度 $0$〜$\theta$ について積分すれば球面部分の面積(図の淡いピンク色部分)、すなわち立体角 $\omega$ が求められます。
$$ \begin{align} \omega &= \int_0^\theta 2 \pi \sin \theta d\theta\\ &= 2 \pi \int_0^\theta \sin \theta d\theta\\ &= 2 \pi \left[ -\cos \theta \right]_0^\theta\\ &= 2 \pi \left( -\cos \theta - ( -\cos0 ) \right)\\ &= 2 \pi ( -\cos \theta + 1 )\\ &= 2 \pi ( 1 -\cos \theta )\\ \end{align} $$
この関係を使って、いくつかの円錐状の立体について、立体角 $\omega$ を求めてみましょう。

$\theta$ が 30° なら、立体角 $\omega_{30}$ は、
$$ \begin{align} \omega_{30} &= 2 \pi(1 - \dfrac{\sqrt{3}}{2})\\ &= \pi (2 - \sqrt{3})\\ &= 0.841…\\ \end{align} $$
$\theta$ が 45° なら、立体角 $\omega_{45}$ は、
$$ \begin{align} \omega_{45} &= 2 \pi(1 - \dfrac{1}{\sqrt{2}} )\\ &= \pi(2 - \sqrt{2})\\ &= 1.840…\\ \end{align} $$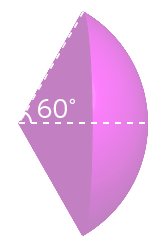
$\theta$ が 60° なら、立体角 $\omega_{60}$ は、
$$ \begin{align} \omega_{60} &= 2 \pi (1 - 0.5)\\ &= \pi\\ &= 3.141…\\ \end{align} $$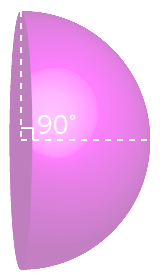
$\theta$ が 90°、つまり半球の立体角 $\omega_{90}$ は、
$$ \begin{align} \omega_{90} &= 2 \pi (1 - 0)\\ &= 2 \pi\\ &= 6.283…\\ \end{align} $$
-
1 sr ってどのくらい?
-
立体角は面積で定義されるので円錐形のものである必要はないのですが、ここでは、身近な円錐形から 1 sr のものを探してみましょう。
お遍路(へん ろ)さんがかぶっている笠(かさ)はどうでしょうか。
お遍路さんというのは、四国にある弘法大師(空海)ゆかりの八十八箇所の霊場を巡礼する人のことです。白衣(びゃく え)に輪袈裟(わ げ さ)を着け、菅笠(すげ がさ)をかぶり、金剛杖(こん ごう づえ)をつく、という特徴的な装束で知られています。


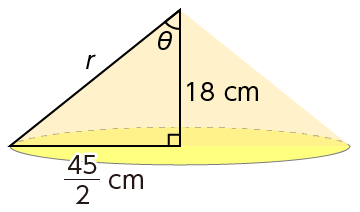
前項で計算した通り、円錐の頂角の半分の大きさ $\theta$ から $\cos \theta$ の値がわかれば、立体角 $\omega$ が求まります。
斜辺を $r$ とおくと、
$$ \begin{align} \cos \theta &= \dfrac{18}{r}\\ &= \dfrac{18}{ \sqrt{ 18^2 + ( \dfrac{45}{2} )^2 }}\\ \end{align} $$よって立体角 $\omega$ は、
$$ \begin{align} \omega &= 2 \pi ( 1 -\cos \theta )\\ &= 2 \pi \left\{ 1 - \dfrac{18}{ \sqrt{ 18^2 + ( \dfrac{45}{2} )^2 }} \right\}\\ &= 2.358…\\ \end{align} $$…およそ 2.4 sr。もう少し尖った形状のようです。
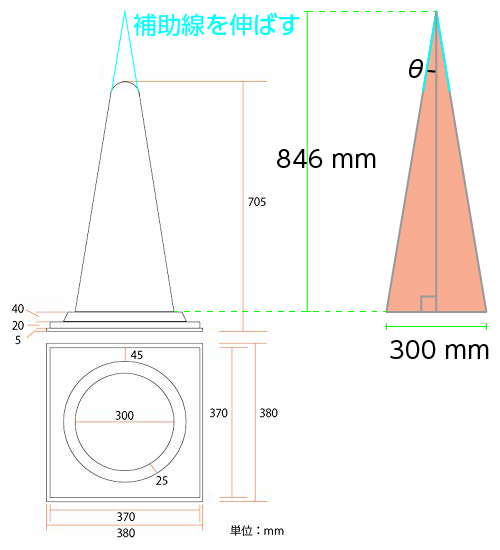
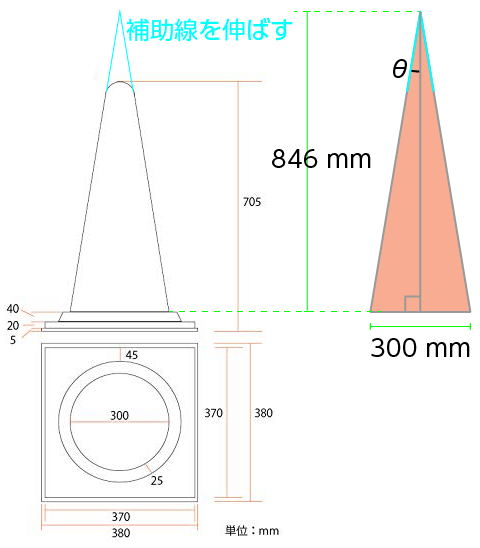
では、道路工事などで見られる三角コーンはどうでしょうか。


図のように補助線を伸ばし、円錐の断面の半頂角から $\cos \theta$ の値を求めてみましょう。
コーンの先の丸み部分を延長してできた円錐の高さは 846 mm になります。
まず、笠のときと同様に $\cos \theta$ を求めます。
$$ \begin{align} \cos \theta &= \dfrac{846}{ \sqrt{ 846^2 + ( \dfrac{300}{2} )^2 } }\\ \end{align} $$よって立体角 $\omega$ は、
$$ \begin{align} \omega &= 2 \pi ( 1 -\cos \theta )\\ &= 2 \pi \left\{ 1 - \dfrac{846}{ \sqrt{ 846^2 + ( \dfrac{300}{2} )^2 } } \right\}\\ &= 0.09649...\ \end{align} $$…およそ 0.1 sr。今度は尖りすぎていました。
笠よりは鋭く、三角コーンよりは鈍い、そんな立体角のもの…
ろ過の実験で使う ろうと はどうでしょうか。


いくつか寸法を当たってみたところ、Tarsons社製のポリロートが 1 sr でした。(ロート 直径35mm (PP製))。
以下のような寸法です。
高さ 77 mm 口内径 35 mm 足長さ 52 mm 足内径 2.8 mm ろ紙を置く部分の立体角 $\omega$ を求めます。
寸法情報から作図すると右下の図のようになります。
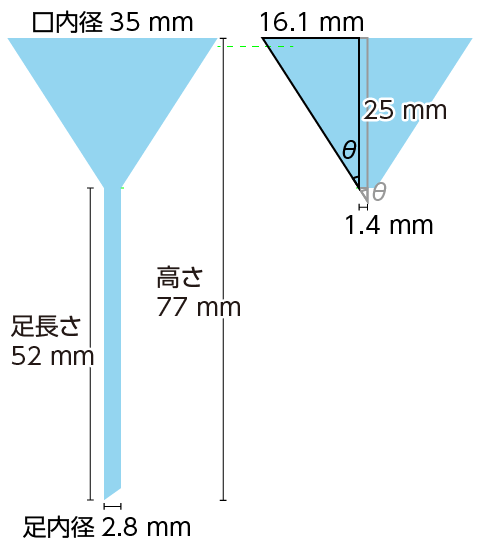
$\cos \theta$ を求めるのに必要な辺の長さは、(35 ÷ 2 − 1.4)= 16.1 mm、
と
77 - 52 = 25 mm
です。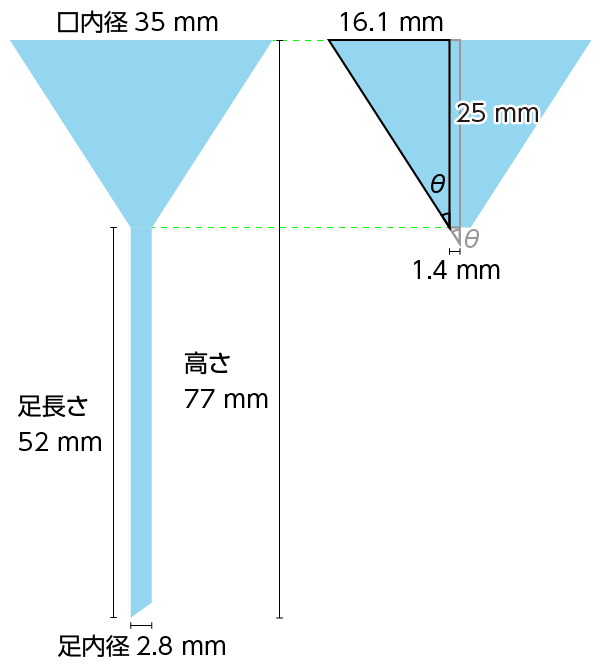
立体角 $\omega$ は、以下のようになります。
$$ \begin{align} \omega &= 2 \pi ( 1 -\cos \theta )\\ &= 2 \pi \left\{ 1 - \dfrac{25}{ \sqrt{ 25^2 + 16.1^2 } } \right\}\\ &= 1.000...\ \end{align} $$みごとに 1 sr です!
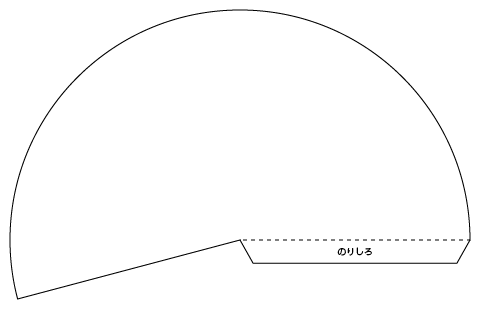
これでも、1 sr のイメージがわかない、という方のために、立体角が 1 sr になる円錐の展開図をご用意しました。プリントアウトして、組み立ててみてください。