

定義:
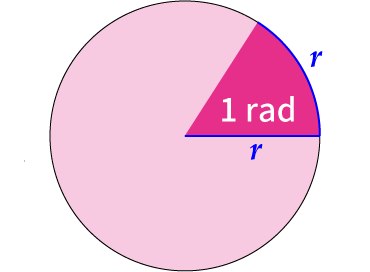
円の半径に等しい長さの弧の中心に対する角度
=単位円(半径1の円)で,長さが1の弧に対する中心角
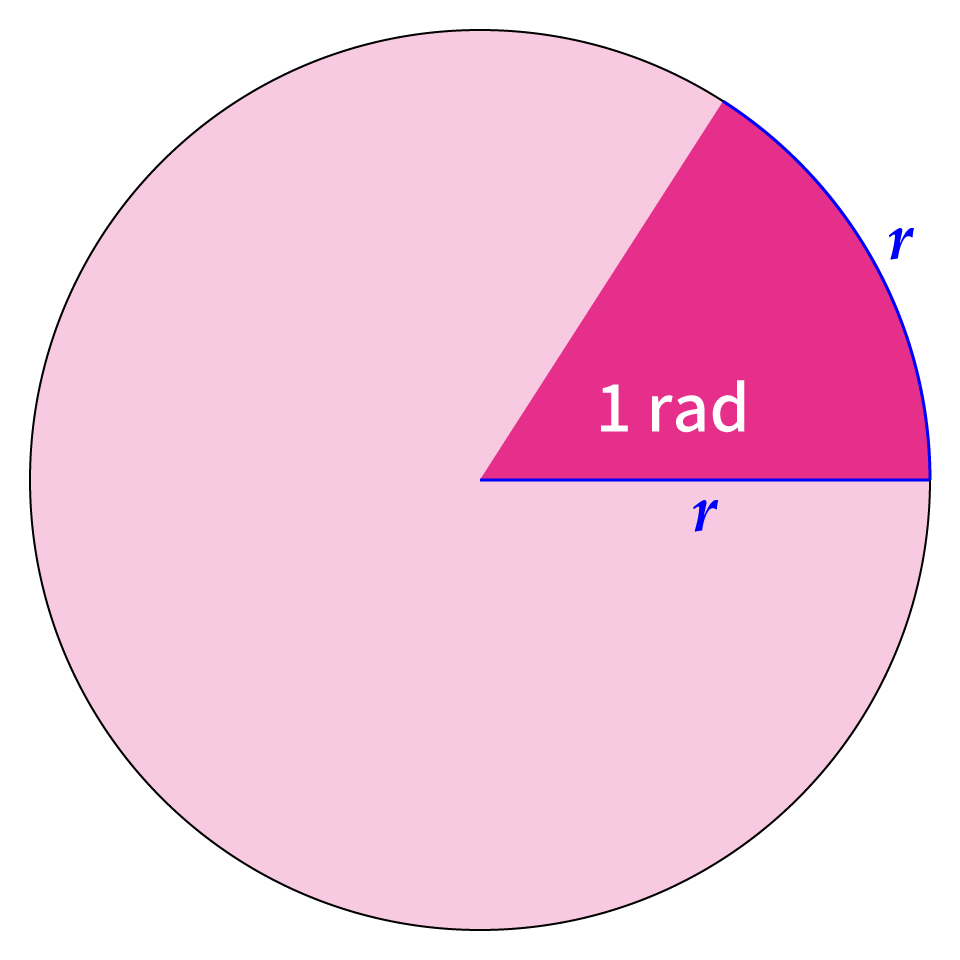
-
単位記号を書かない単位
-
rad は,半径という意味のラテン語 radius に由来する単位で,高校以降で登場しますが,あまり rad の記号を目にすることはありません。
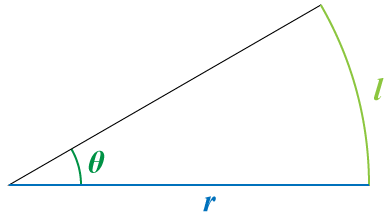
半径 $r$ の円に弧 $l$ があるとき,この弧に対応する中心角 $\theta$ を rad で求めてみます。
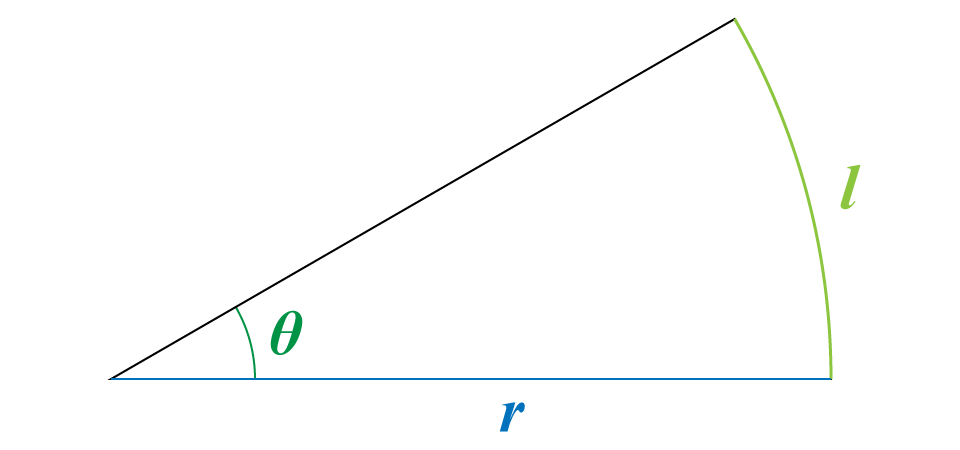
定義より,1 rad は,半径の長さと等しい長さの弧に対する中心角なので,$\theta$ = $\cfrac{l}{r}$ rad となります。
ここで,$l$ も $r$ も長さなので,分子と分母の単位が打ち消しあってなくなります。このため,記号を明示する必要がある場合をのぞいて,ふつう rad は省略して表記します。例えば,「角度が 90°」なら,「角度が $\cfrac{\pi}{2}$ rad」とはせず,単に「角度が $\cfrac{\pi}{2}$」と書きます。
-
rad と ° の関係
-
円周の長さは,直径×円周率で求められるので,半径 $r$ の円の円周 $l$ は,$2\pi r$ となります。定義から,これを半径の $r$ で割った $2\pi$ が,1周分の角度となります。
$2\pi \,\text{rad} = 360^{\circ}$いくつかの代表的な角度について rad の値を表にしました。
度
°0 30 45 60 90 120 135 150 180 270 360 ラジアン
rad0 $\cfrac{\pi}{6}$ $\cfrac{\pi}{4}$ $\cfrac{\pi}{3}$ $\cfrac{\pi}{2}$ $\cfrac{2\pi}{3}$ $\cfrac{3\pi}{4}$ $\cfrac{5\pi}{6}$ $\pi$ $\cfrac{3\pi}{2}$ $2\pi$ 度〔°〕 ラジアン〔rad〕 0 0 30 $\cfrac{\pi}{6}$ 45 $\cfrac{\pi}{4}$ 60 $\cfrac{\pi}{3}$ 90 $\cfrac{\pi}{2}$ 120 $\cfrac{2\pi}{3}$ 135 $\cfrac{3\pi}{4}$ 150 $\cfrac{5\pi}{6}$ 180 $\pi$ 270 $\cfrac{3\pi}{2}$ 360 $2\pi$ このように rad は,ふつう $\pi$ を無理に計算せずに分数の形のままで扱います。
-
rad を使う利点
-
rad による角度の表記は,弧の長さによって角度を示すことから弧度法といいます。これに対して,小学校から親しんで来た1周を 360° とする単位は,度数法といいます。
弧度法と度数法をいくつかの場面で比較してみます。
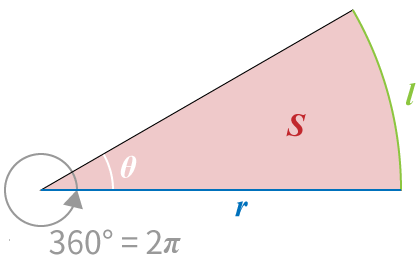
①おうぎ形の弧の長さ
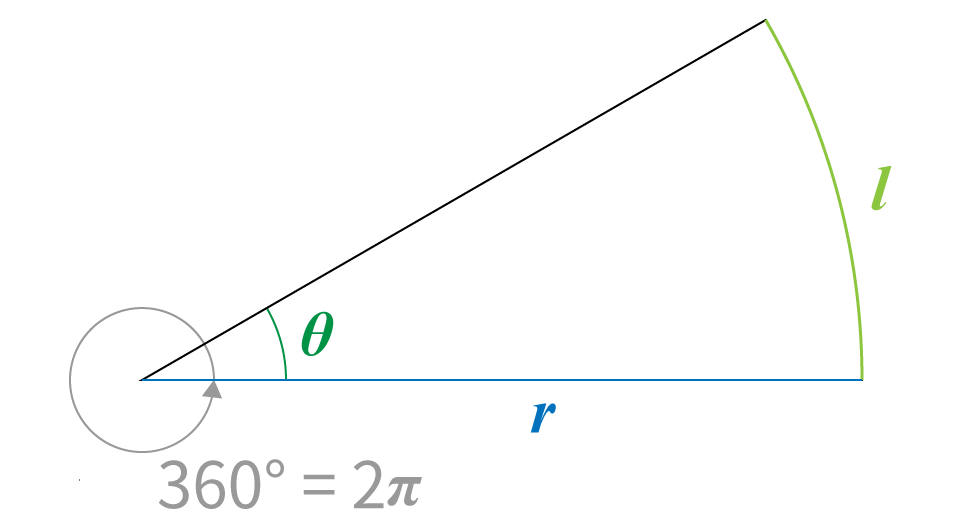
半径 $r$,中心角 $\theta$ のおうぎ形の弧の長さ $l$ を求めてみましょう。
おうぎ形の弧の長さは,円周の長さに $\cfrac{\text{中心角}}{1周分の角} $ をかけて求められます。$$ \begin{align} \text{度数法:} l &= 2 \pi r \times \frac{\theta^{\circ}}{360^{\circ}}\\ &= \frac{\pi r \theta}{180}\\ \text{弧度法:} l &= 2 \pi r \times \frac{\theta}{2\pi}\\ &= r \theta\\ \end{align} $$②おうぎ形の面積
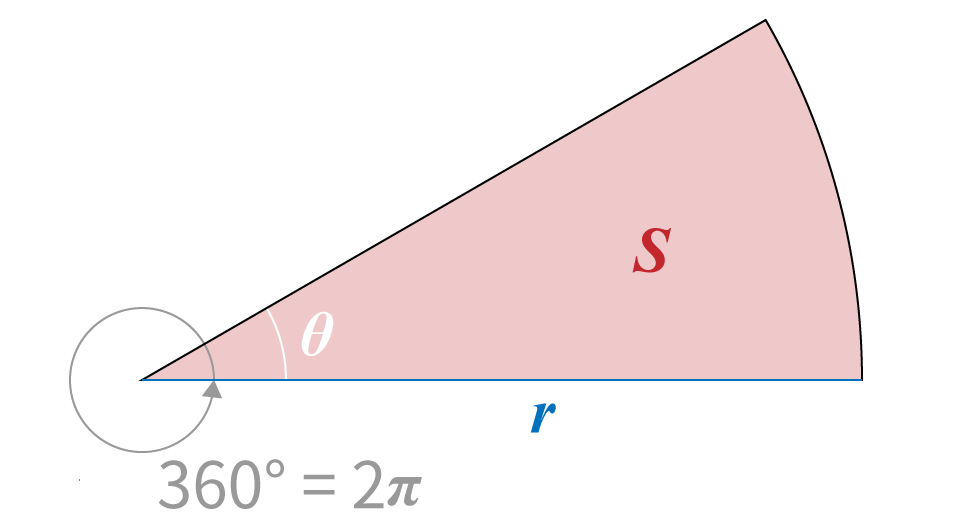
今度は,面積 $S$ を求めてみましょう。
おうぎ形の面積は,円の面積に $\cfrac{\text{中心角}}{1周分の角} $ をかけて求められます。$$ \begin{align} \text{度数法:} S &= \pi r^2 \times \frac{\theta^{\circ}}{360^{\circ}}\\ &= \frac{\pi r^2 \theta}{360}\\ \text{弧度法:} S &= \pi r^2 \times \frac{\theta}{2 \pi}\\ &= \frac{r^2 \theta}{2}\\ \end{align} $$弧度法を使うと,おうぎ形についての公式がかなりスッキリしますね。
③三角関数
rad が威力を発揮するのは,高校で学習する三角関数($\sin \theta$,$\cos \theta$,$\tan \theta$)を使った計算をするときです。
高校の数学では,関数の極限を求めたり,微分・積分という計算をしたりします。なかでも,三角関数の極限を考えるときには,$\cfrac{\sin \theta}{\theta}$ という形が鍵になります。
さらに,三角関数を微分するときは,$\cfrac{\sin \theta}{\theta}$ の極限($\displaystyle \lim_{\theta \to 0 }\cfrac{\sin \theta}{\theta}$ の値)を使った計算が必要になります。
(詳しい計算は高校数学の学習に任せることにして…)
三角関数の極限と微分の計算に使う重要な公式を,それぞれ度数法と弧度法で表すと,次のようになります。$$ \begin{alignat}{2} \text{度数法 } && \text{極限:}&& \displaystyle \lim_{\theta \to 0} \frac{\sin \theta}{\theta} &= \frac{\pi}{180}\\ && \text{微分:}&& (\sin \theta)' &= \frac{\pi}{180} \cos \theta\\ &&&& (\cos \theta)' &= - \frac{\pi}{180} \sin \theta\\ \text{弧度法 } && \text{極限:}&& \displaystyle \lim_{\theta \to 0} \frac{\sin \theta}{\theta} &= 1\\ && \text{微分:}&& (\sin \theta)' &= \cos \theta\\ &&&& (\cos \theta)' &= - \sin \theta\\ \end{alignat} $$弧度法の公式の方が,余計な係数がなくスッキリしていて,使いやすそうですね。
-
1 rad ってどのくらい?
-
春分・秋分の日の長崎市(と熊本市)における太陽の南中高度が,約 1 rad です。
春分・秋分では,赤道において太陽が天頂を通過する(南中高度が 90° = $\cfrac{\pi}{2}$ rad になる)ので,北緯 $\theta$ の地点における春分・秋分の日の南中高度は $\cfrac{\pi}{2} - \theta$ となります。
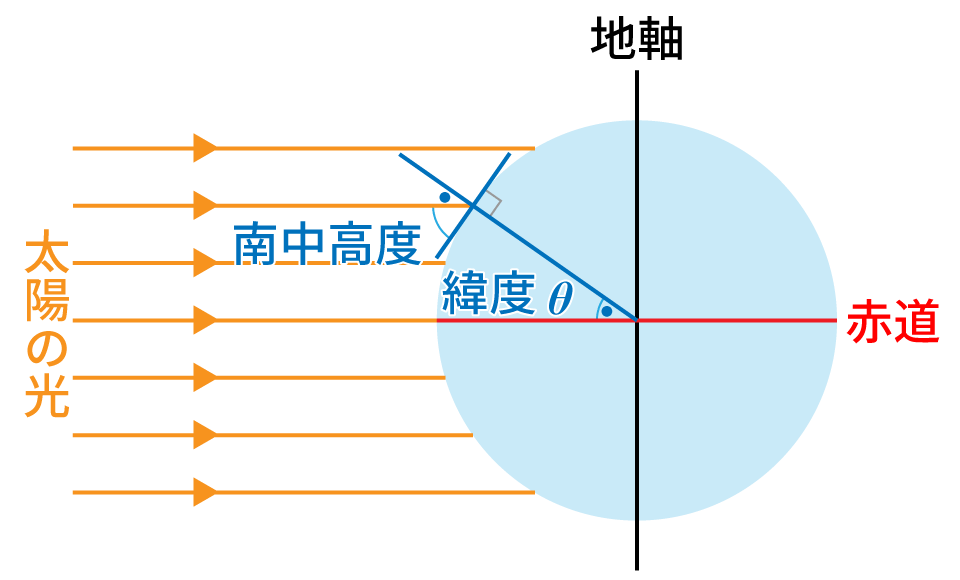
よって,南中高度が 1 rad となる緯度は,次のように求められます。
$$ \begin{align} \frac{\pi}{2} - \theta &= 1 \,\text{rad}\\ \theta &= \frac{\pi}{2} - 1 \,\text{rad}\\ \text{これを度}&\text{数法の角度に直すと}\\ \theta &= (\frac{\pi}{2} - 1 ) \times \frac{360^\circ}{2\pi}\\ &= 32.7042\ldots^\circ\\ \end{align} $$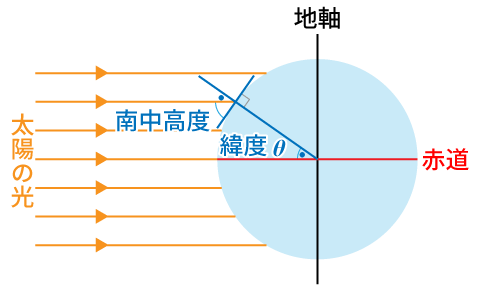
北緯 32.7° の地点を日本地図から探すと,長崎市が近そうです。
国立天文台の各地のこよみで調べてみると,長崎の緯度は 32.7500°,春分・秋分の日の南中高度はいずれも 57.3° とあります。これを rad に直すと,次のようになります。
$$ \begin{align} 2 \pi : x &= 360^\circ : 57.3^\circ\\ x &= \frac{2 \pi \times 57.3^\circ}{360^\circ}\\ &= 1.000073661\ldots \,\text{rad}\\ \end{align} $$天文台のデータから,ほかの都市で南中高度が 約 1 rad となる日にちを調べると,次のようになりました。
南中高度が 1 rad となる日(2019年秋)
都市 日 時刻 南中高度 札幌(北海道) 8月27日 11:36 57.1° 根室(北海道) 8月26日 11:20 57.2° 青森(青森県) 9月2日 11:37 57.3° 秋田(秋田県) 9月5日 11:38 57.3° 盛岡(岩手県) 9月5日 11:34 57.3° 仙台(宮城県) 9月9日 11:34 57.2° 山形(山形県) 9月9日 11:36 57.2° 福島(福島県) 9月10日 11:35 57.3° 水戸(茨城県) 9月14日 11:34 57.2° 宇都宮(栃木県) 9月13日 11:37 57.4° 前橋(群馬県) 9月14日 11:40 57.2° さいたま(埼玉県) 9月15日 11:37 57.3° 千葉(千葉県) 9月16日 11:35 57.2° 東京(東京都) 9月16日 11:36 57.1° 横浜(神奈川県) 9月16日 11:36 57.4° 小笠原(東京都) 10月8日 11:19 57.2° 新潟(新潟県) 9月10日 11:41 57.2° 富山(富山県) 9月13日 11:47 57.3° 金沢(石川県) 9月13日 11:50 57.4° 福井(福井県) 9月15日 11:51 57.1° 甲府(山梨県) 9月16日 11:41 57.1° 長野(長野県) 9月13日 11:43 57.3° 岐阜(岐阜県) 9月16日 11:48 57.4° 静岡(静岡県) 9月18日 11:41 57.1° 名古屋(愛知県) 9月17日 11:47 57.3° 都市 日 時刻 南中高度 津(三重県) 9月18日 11:48 57.3° 大津(滋賀県) 9月17日 11:51 57.4° 京都(京都府) 9月17日 11:52 57.4° 大阪(大阪府) 9月18日 11:52 57.3° 神戸(兵庫県) 9月18日 11:54 57.3° 奈良(奈良県) 9月18日 11:51 57.3° 和歌山(和歌山県) 9月19日 11:53 57.4° 鳥取(鳥取県) 9月16日 11:58 57.3° 松江(島根県) 9月16日 12:03 57.3° 岡山(岡山県) 9月18日 11:59 57.4° 広島(広島県) 9月19日 12:04 57.3° 山口(山口県) 9月20日 12:08 57.1° 徳島(徳島県) 9月20日 11:55 57.2° 高松(香川県) 9月19日 11:58 57.3° 松山(愛媛県) 9月20日 12:03 57.4° 高知(高知県) 9月21日 11:59 57.3° 福岡(福岡県) 9月21日 12:12 57.3° 佐賀(佐賀県) 9月22日 12:12 57.2° 長崎(長崎県) 9月23日 12:13 57.3° 熊本(熊本県) 9月23日 12:10 57.3° 大分(大分県) 9月22日 12:06 57.2° 宮崎(宮崎県) 9月25日 12:06 57.4° 鹿児島(鹿児島県) 9月26日 12:09 57.3° 那覇(沖縄県) 10月10日 12:16 57.3°
-
単位の換算
-
空欄に数値入力することで、単位を換算することができます。
$\text{ rad}$ = $\text{°}$


