積や商を線分で表すと…

　小学校では 2＋3=5 や 5－2=3 などの計算をしました。この計算は，線分を使って表すことも
できます。

　同じように，積や商はどのような線分として表せるのでしょうか。

　まずは，$ab$ の長さの線分を表します。

　この長さは，比を使って表すと，

$a : 1 = x : b$

となる $x$ の長さになります。相似の考えを使って，この $x$ を図で表してみましょう。

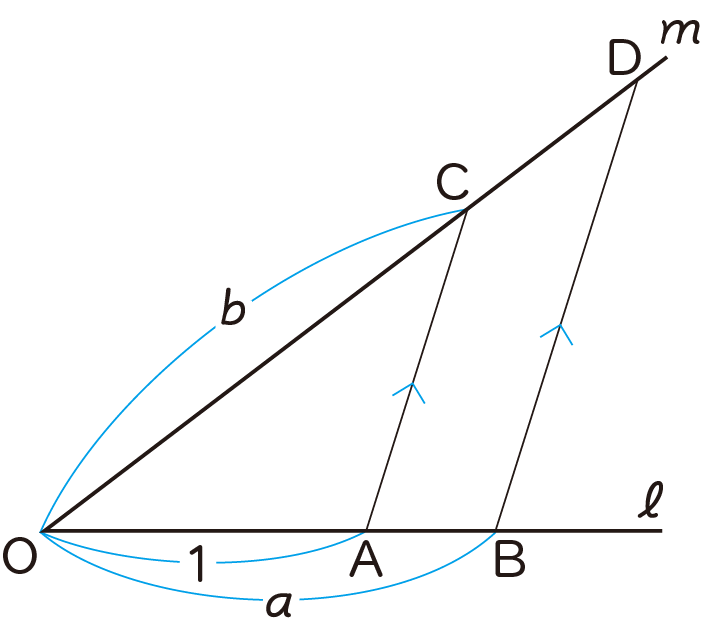
　右上の図のように，直線 $\ell$ 上に OA=1 となる点Aをとり，
次に点Bをとって OB=$a$ とします。
また，直線 $m$ 上に点Cをとり，OC=$b$とします。

　点Bを通りACに平行な直線をひき，
直線 $m$ との交点をDとすると，
△DOB∽△COAとなることから，
　OD：OC = OB：OA
つまり，OD：$b$ = $a$：1

　よって，OD = $ab$ となります。

　今度は，同じように相似の考えを使って，$\dfrac{a}{b}$の長さの線分も表します。

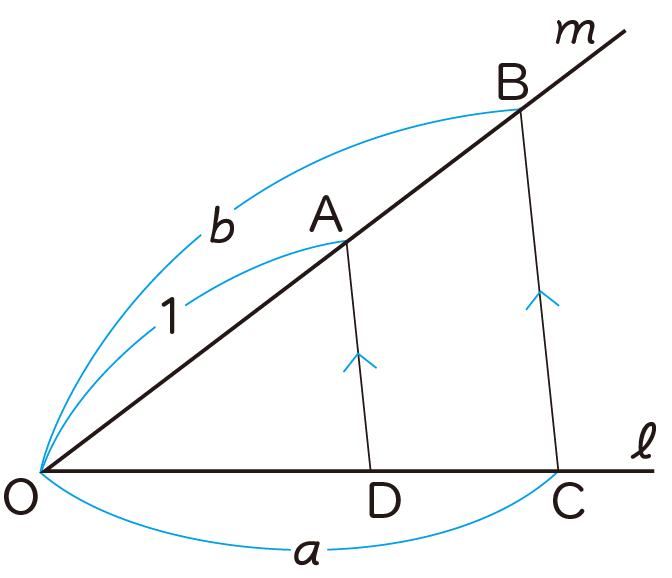
　右の図のように，直線 $m$ 上に OA = 1，OB = $b$ となる
点A，Bをとり，直線 $\ell$ 上に OC = $a$ となる点Cをとります。

　点Aを通り，BCに平行な直線をひき，$\ell$ との交点をDと
すると， △BOC∽△AODだから，

　　OB：OA = OC：OD　
つまり，$b$：1 = $a$：OD

　よって，OD = $\dfrac{a}{b}$ となります。