リレーのバトンパス

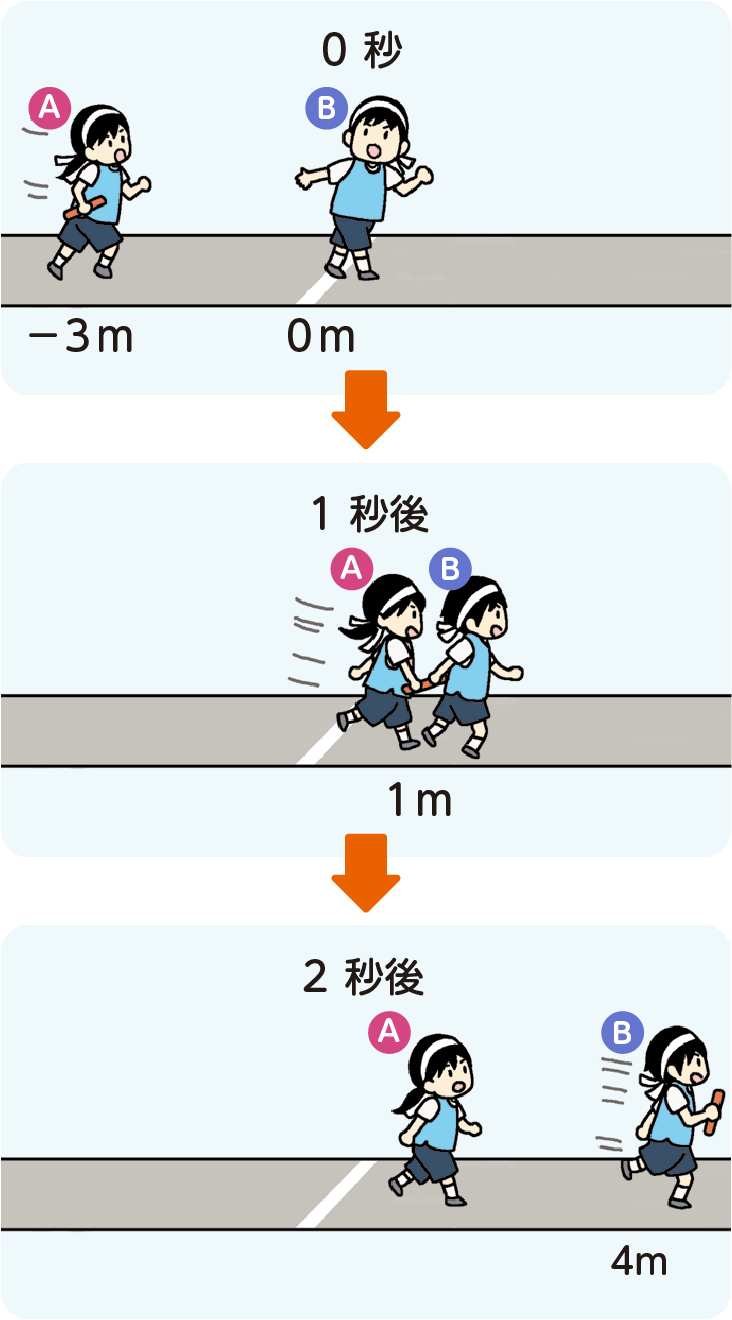
　体育大会などで行われるリレーでは，バトンパスがとても重要です。ここでは，関数のグラフを使って，バトンパスについて考えてみましょう。

　右下の図のように，走者A が次の 走者B にバトンパスをします。Bがスタートする瞬間を0秒，そのときのBの位置を0 mとして，$x$ 秒後の走者の位置を $y$ mとします。

　Bはスタートしてからどんどん加速していきます。ここでは，1秒後に 1 m，2秒後に 4 m，3秒後に 9 mと進むとすると，$x$ と $y$ の関係は $y=x^2$ で表せます。

　一方，Aは，ほぼ一定の速さで走ってくると考えられます。3 m 手前から1秒間に4 m ずつ進むとすると $x$ と $y$ の関係は1次関数の式 $y=4x−3$ で表せます。

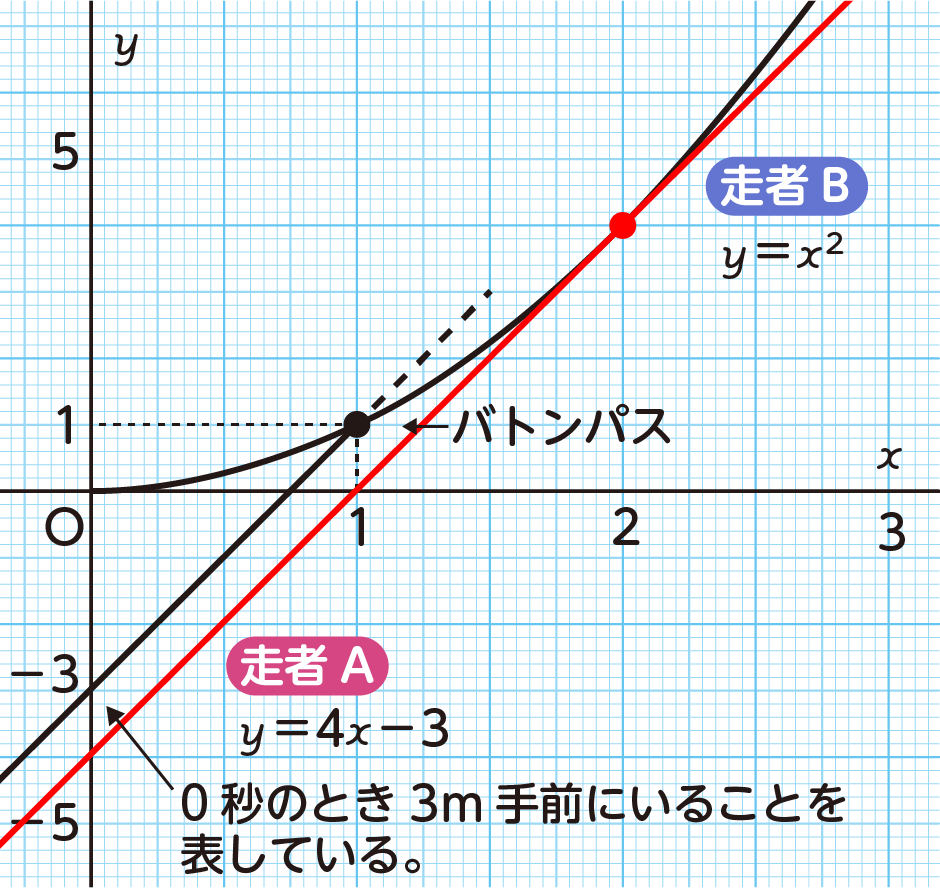
　これらの式をグラフに表すと，左下のようになります。このグラフでは，バトンパスが行われる位置がグラフの交点として表されています。

　ところで，バトンパスでは，Aができるだけ手前にいるときにBがスタートするほうが有利です。上の例では，Bがスタートするとき，Aが最大で何m離れた位置までであれば，バトンパスを行うことができるでしょうか。Aのグラフの切片を変えて，グラフをかいて調べてみます。
　2枚の定規を使って、$y=4x−3$ のグラフと平行な直線を動かして考えると，$y=4x−4$ のとき，$y=x^2$ との交点が1つになります。これは，Bがスタートして2秒後に 4 ｍ進んだ地点でバトンパスができます。しかし、$y=4x+b$ で，$b < −4$ のとき，$y=x^2$ とは交わりません。したがって，走者Ａが最大で 4 m離れた位置までであれば，バトンパスができることが，グラフからわかります。