おかしな証明
次の証明は、「すべての三角形は二等辺三角形である」ことの証明です。
[証明]
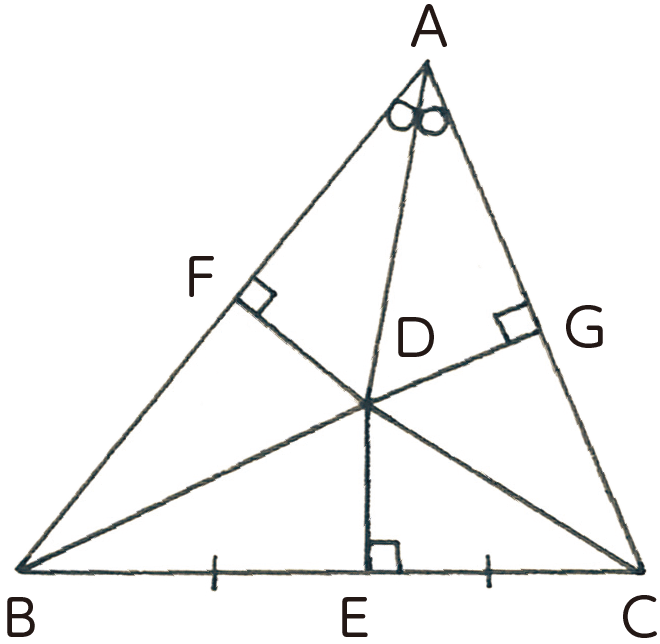
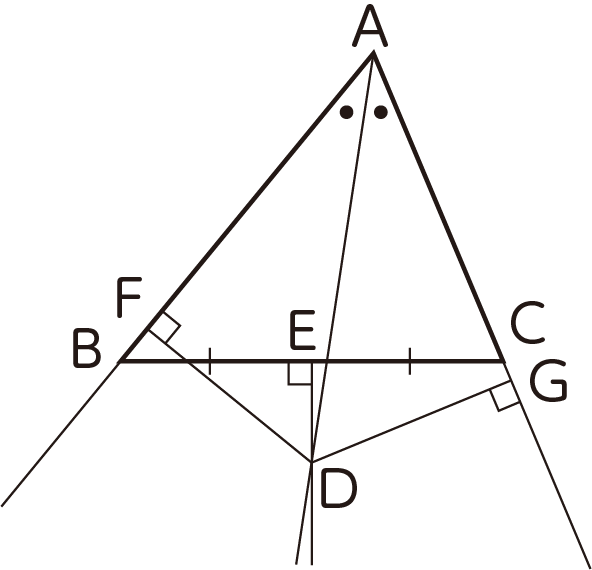
∠Aの二等分線と辺BCの垂直二等分線との交点をDとする。
また,辺BCの垂直二等分線と辺BCとの交点をEとする。
Dから辺AB,ACに垂線DF,DGをひくと,
△ADF≡△ADG ……… ①
△DEB≡△DEC ……… ②
①,②より,合同な直角三角形の対応する辺だから,
DF=DG,DB=DC
よって,
△DFB ≡ △DGC ……… ③
①より,AF=AG ……… ④
③より,FB=GC ……… ⑤
④,⑤よりAF+FB=AG+GC
したがって,
AB=AC
しかし,すべての三角形が二等辺三角形であるはずがありませんから,どこかがまちがっているはずです。
このおかしな「証明」は,どこがまちがっているのでしょうか。