証明とは

　数学では，あることがらが正しいことを示すのに，実測や実験ではなく，証明という方法を使います。

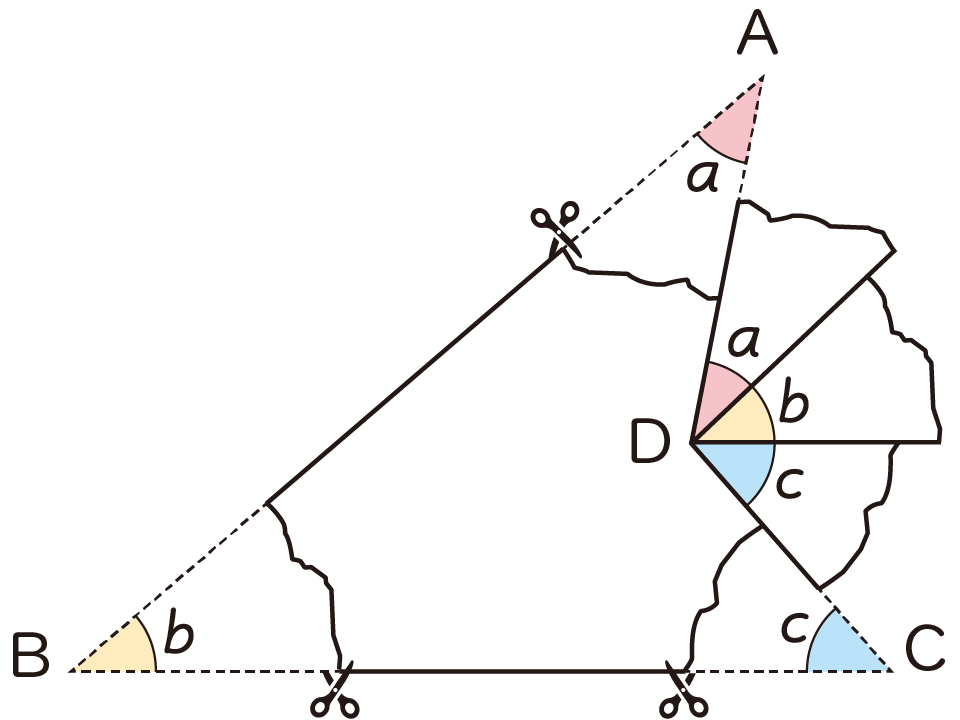
　たとえば，「くさび形ABCDで，
∠A＋∠B＋∠C＝∠ADCである」ことは，
角を測ったり，紙を切って並べたりする実測や実験による方法で予想することができます。
しかし，このような実測や実験による方法では，「『どんなくさび形でも，』
∠A＋∠B＋∠C＝∠ADCである」といい切ることは
できません。

　私たちは，証明という方法を使うことで，論理的に，どんな場合でもそのことがらが成り立つ
ことを示すことができます。そして，証明を示すことで，だれにでも納得してもらうことができるのです。

　どんなに正しいと思うことがらでも，
　　「いつでもいえるのだろうか。」
　　「ほかの場合は考えられないだろうか。」
　　「根拠を明らかにしよう。」
などと考えてみましょう。このような見方が，証明をする際に
とても大切です。

　証明を大事にするということは，人に納得してもらうためということと同時に，ものごとを自分できちんとすじ道を立てて考えてみるという態度そのものでもあります。数学では1つ1つのことがらに対し，根拠をはっきりとさせながら先へ進むことが大切なのです。