ディオファントスの方程式

　3世紀ごろ，ギリシャに方程式の研究をしているディオファントスという人がいました。彼の墓碑には，次のような文章が刻まれていたといわれています。

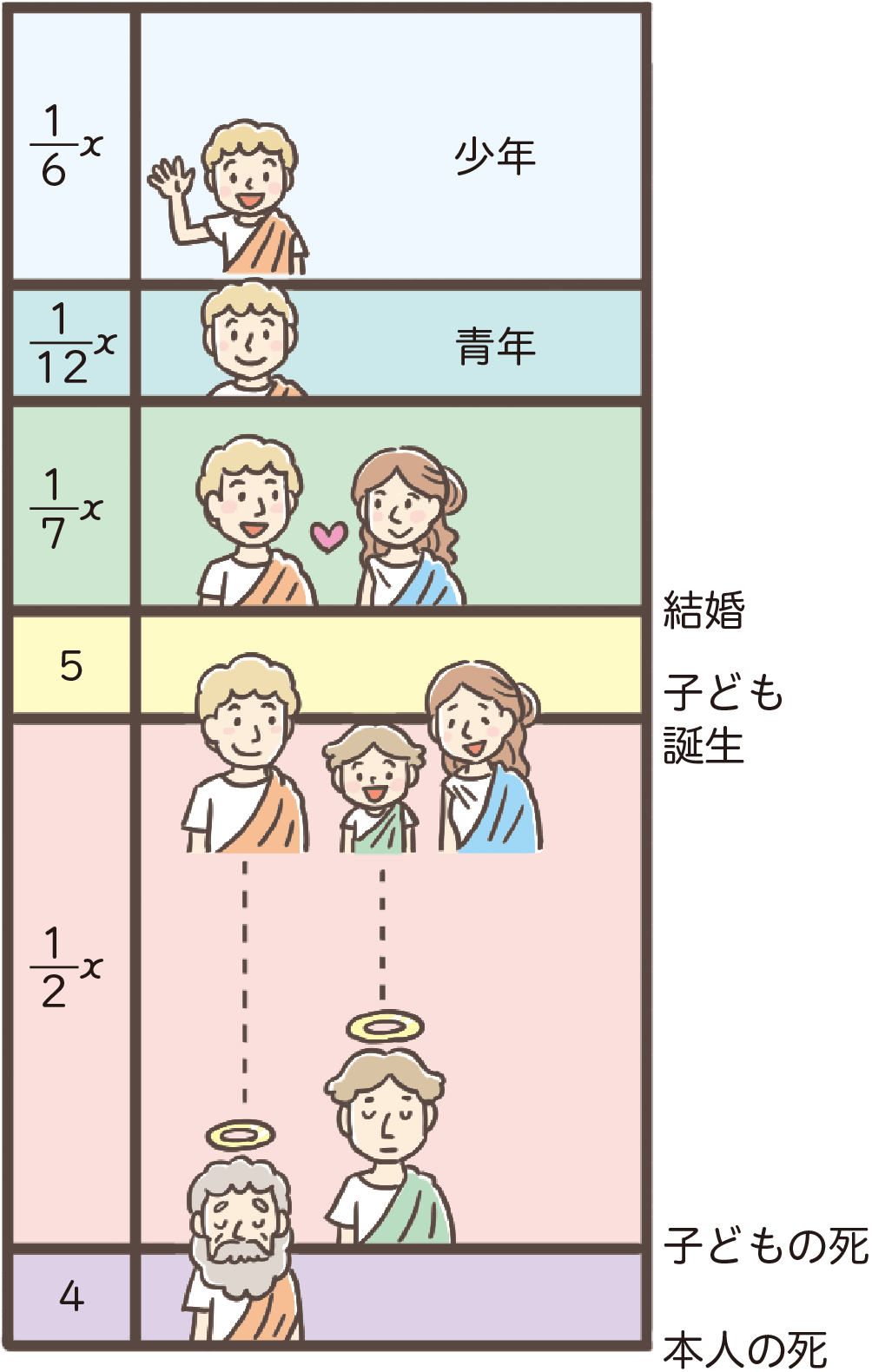
「ディオファントスは，その生涯の$\dfrac{1}{6}$を少年として，$\dfrac{1}{12}$を青年として，その後，生涯の$\dfrac{1}{7}$を独身で過ごした。結婚して5年後に息子が生まれたが，この息子は父の生涯の半分だけ生きた。父はその子の死の4年後にこの世を去った。」

　ディオファントスがなくなった年齢を $x$ 歳とすると，彼の息子は $\dfrac{1}{2} x$ 歳でこの世を去ったことになります。
したがって，この文章を式にすると，次のようになります。

$\dfrac{1}{6} x + \dfrac{1}{12} x +\dfrac{1}{7} x + 5 + \dfrac{1}{2} x + 4 = x$

　この方程式を解くと，ディオファントスがなくなった年齢を求めることができます。
ディオファントスはいくつでなくなったのでしょうか。