平均の平均は全体の平均?
小学校では,平均値,最頻値,中央値などの代表値を学びました。そして,中学校では,階級値を学びました。
平均は「ならして考える」ということからわかりやすく,広く利用されています。たとえば,次の表はバスケットボール部の生徒がシュートを10回したときの成功数を調べた資料です。1年生部員の平均値と2年生部員の平均値を比べると,2年生のほうが値が大きいことがわかります。
| 生徒番号 | 成功数 |
|---|---|
| 1 | 2 |
| 2 | 5 |
| 3 | 3 |
| 4 | 7 |
| 5 | 5 |
| 6 | 6 |
| 7 | 3 |
| 8 | 9 |
| 9 | 8 |
| 10 | 3 |
| 合計 | 51 |
| 平均値 | 5.1 |
| 生徒番号 | 成功数 |
|---|---|
| 1 | 4 |
| 2 | 9 |
| 3 | 8 |
| 4 | 7 |
| 5 | 5 |
| 6 | 7 |
| 7 | 8 |
| 8 | 5 |
| 9 | 6 |
| 10 | 7 |
| 11 | 7 |
| 12 | 3 |
| 13 | 6 |
| 14 | 9 |
| 15 | 8 |
| 合計 | 99 |
| 平均値 | 6.6 |
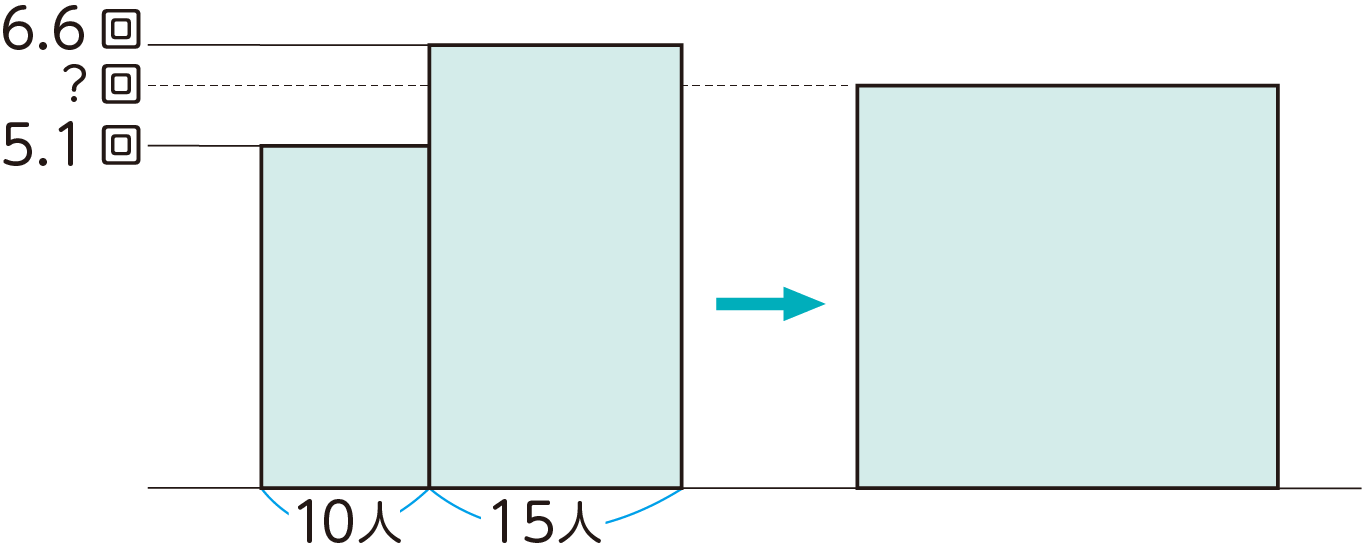
このバスケットボール部の1年生と2年生をまとめた全体の平均値はどのように求められる
でしょうか。Aさんは,1年生の平均値と2年生の平均値を使って,次のように求めました。
Aさんの考え
1年生の平均値は5.1回,2年生の平均値は6.6回
だから,(5.1+6.6)÷ 2 = 5.85
したがって,全体の平均値は5.85回
Aさんの求め方は正しいように見えますが,実は正しくありません。正しい求め方は,次のようになります。
正しい考え方
成功数の合計は,51+99=150(回)
人数の合計は,10+15=25(人)
だから,150÷25=6
したがって,全体の平均値は6回