データを正しく活用するには

　テレビや新聞，ウェブサイトなどで，これまでに学習したさまざまなグラフを見ることがあると思います。生活のなかにあふれるグラフを読むときには注意が必要な場合もあります。
どのような点に注意するとよいのでしょうか。

グラフの見せ方

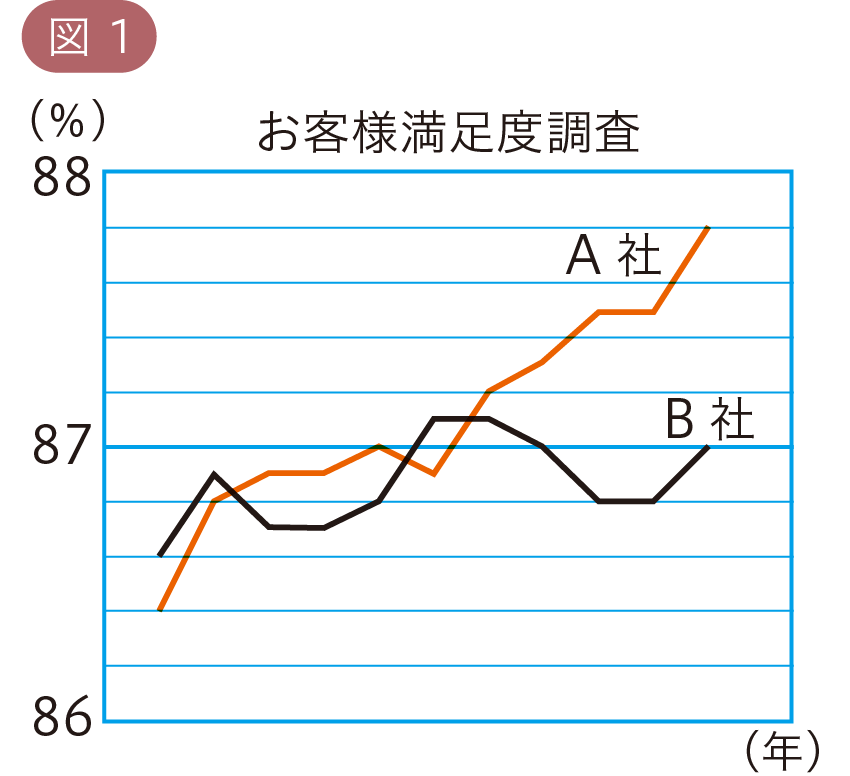
　図1のグラフは，ある会社A社が「お客様満足度」の推移を，ライバル会社B社と比較し，
作成したグラフです。このグラフを見て，あなたはどのような印象をもちますか。
　このグラフは，一見するとA社の満足度がますます高くなり，B社を大きくひき離していくように見えますが，実際にはA社が87.8％，B社が87％で，0.8％しかちがいはありません。
グラフの縦軸が86％〜88％の2％しか示されていないため，ちがいが大きく見えるのです。
　これを，図2のようなグラフにつくり変えると，2社のちがいはほとんどないことがわかります。

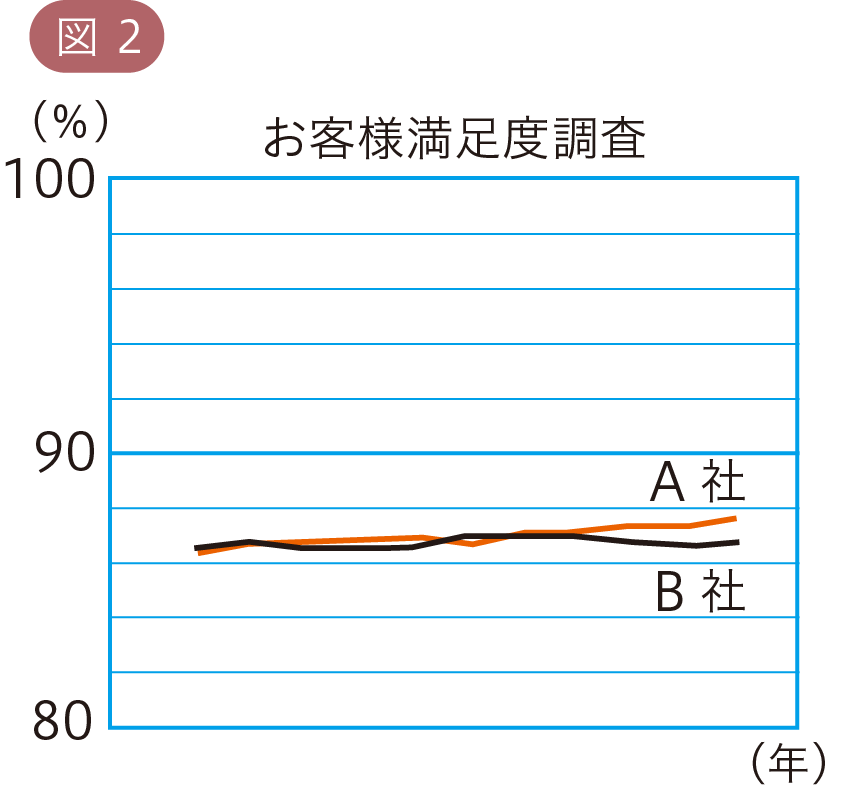
　このように，グラフの見せ方を変えることで，相手に与える印象を操作することができるので，
グラフを読み取るときには，縦軸や横軸のとり方などを確認する必要があります。逆に，グラフを使って何かを示すときには，誤解を与えないように注意する必要があります。

データの集め方

　グラフを読み取るときには，グラフのもととなるデータをどのように集めたかを確認することも
大切です。
　たとえば，図1，2のグラフの「お客様満足度」は，どのような人に調査した結果なのでしょうか。これが，A社の商品を長年使っている人のみに調査したのであれば，「満足しているから，A社の商品を使い続けている」という人が多い可能性もあるため，適切な調査とはいえません。また，調査した人数も不明です。もし人数が少ない場合は，全体の傾向を正しく示すことができていない場合もあります。
　このように，データを読み取るときは，そのデータがどのような調査をもとにしているのかを
知っておく必要があります。

代表値の使い方

　代表値の使い方についても考えてみましょう。
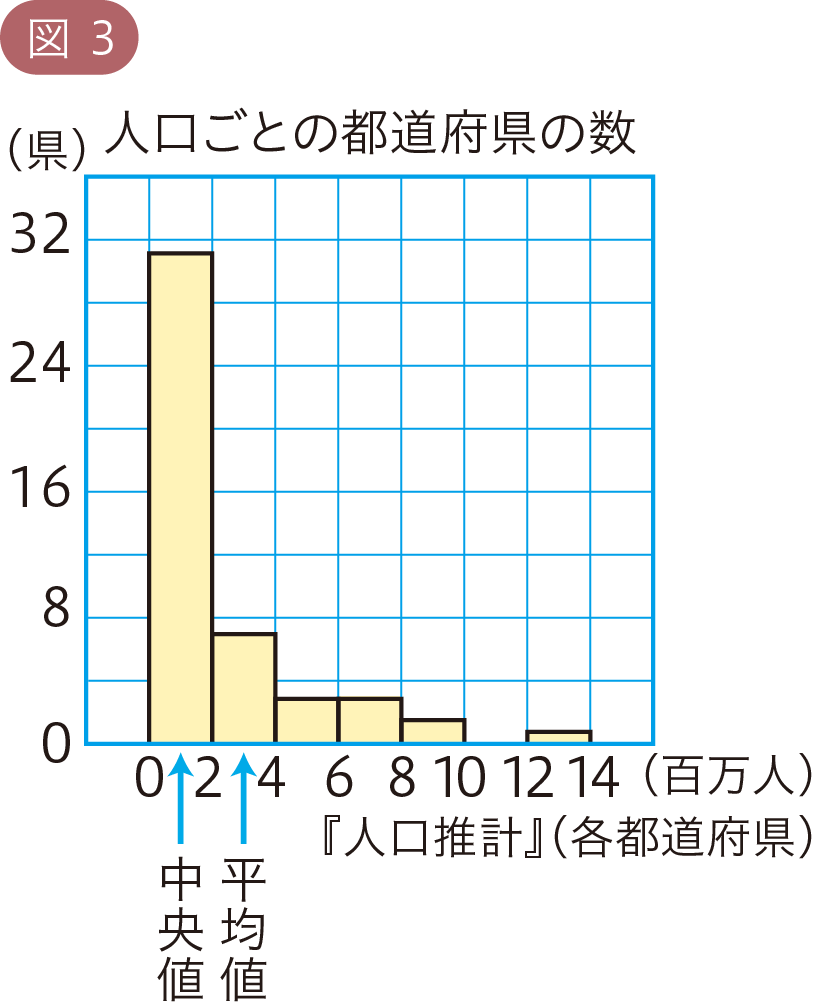
　たとえば，2022年の各都道府県の人口の平均値は，およそ266万人です。このことから，「人口270万人くらいの都道府県が多い」と考えてよいでしょうか。

　図3のように，人口ごとの都道府県の数をヒストグラムに表してみると，平均値をふくむ階級（200万人以上400万人未満）の度数は，あまり多くありません。一方，中央値はおよそ156万人で，この値がふくまれる階級の度数が多くなっています。

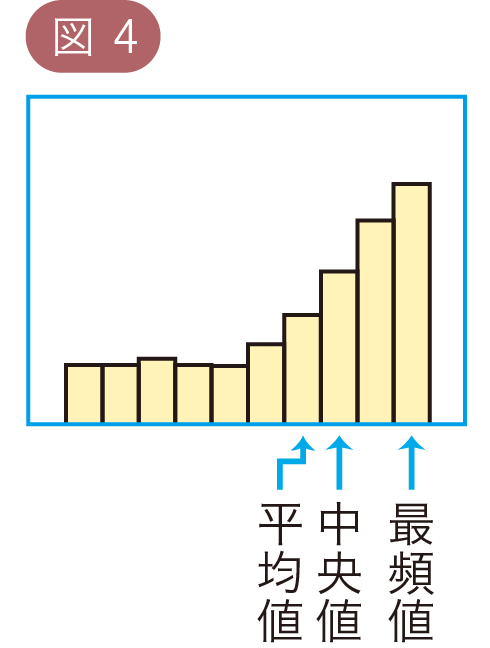
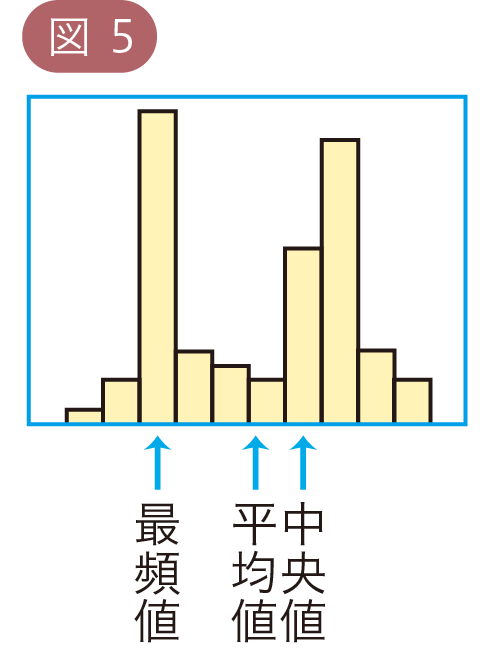
　また，最頻値についても，図4のように，平均値，中央値とは離れた値になったり，図5のように山が2つあるグラフでは，一方の山の傾向しか表せなかったりします。このようなデータの分布のちがいにも注意して，目的に合った代表値を選ぶことが大切です。