０の発見と負の数の誕生

　数を表す方法を「記数法」といいます。現在使われている記数法が発見されるまでは，
次のように国や時代によってさまざまな記数法が使われていました。

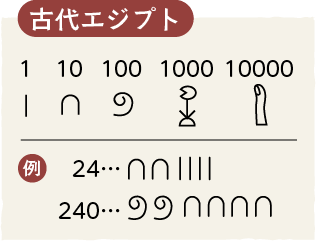
　古代エジプトや古代中国の記数法では，大きな数を表すたびに新しい記号が必要になるため，
大変不便でした。一方，古代インドでは，0を使った記数法が発見されました。数が置かれた
場所によって位を表す「位取り」という考え方と，位に何もないことを表す「0」という数の
発見によって，私たちはたった10個の数字（0，1，2，3，4，5，6，7，8，9）で，
どんな数でも表せるようになりました。

　では，0より小さい負の数は，どこで，どのようにして生まれたのでしょうか。

　負の数を認めた最初の人は，0の発見者でもあるインドの人といわれています。

　中国でも紀元前から，負の数が使われていたようです。中国では，数の計算に「算木」とよばれる細長い直方体の形をした計算用具が使われていました。算木は赤と黒の2色に着色され，
赤は正の数を，黒は負の数を表していました。

　インドでも7世紀ごろには，負の数を使った計算が行われていました。
ブラーマグプタ（598〜660）は，正の数を財産，負の数を借金という考えに結びつけたり，
方向が互いに反対であるものに対して使ったりしました。しかし，このような意味でしか
使われなかったため，（負の数）×（負の数）が理解されませんでした。

　一方，ヨーロッパでは，負の数は「不条理な数」，「無いものより小さい数」と考えられ，
その存在は，長い間否定し続けられてきました。負の数が数として認められたのは，
17世紀になってからのことです。フランスの数学者であり，哲学者でもあったデカルト
（1596〜1650）が座標の考えを発見したことがそのきっかけとなりました。